HOW TO CHECK WHICH TYPE OF DECIMAL EXPANSION

Question 1 :

Express the following rational numbers into decimal and state the kind of decimal expansion

(i) 2/7

Solution :

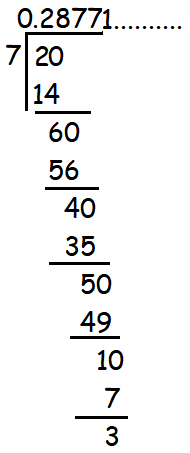
2/7  =  0.28771...........

Hence the given fraction will have non terminating and recurring decimal expansion.

(ii)  -5  3/11

Solution :

-5  3/11  =  - (55 + 3)/11  =  -58/11

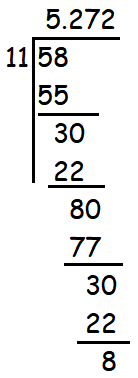
-58/11  =  5.2727..........

Hence the given fraction will have non terminating and non recurring decimal expansion.

(iii)  22/3

Solution :

22/3  =  

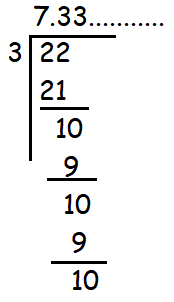
Hence the given fraction will have non terminating and recurring decimal expansion.

(iv)  327/200

Solution : 

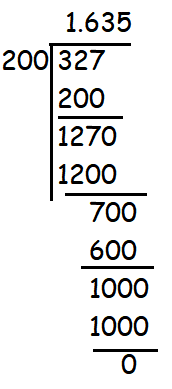
Hence the given fraction will have terminating decimal expansion.

How to Find Length of Period of Decimals

Question 2 :

Express 1/13 in decimal form. Find the length of the periods of decimals.

Solution :

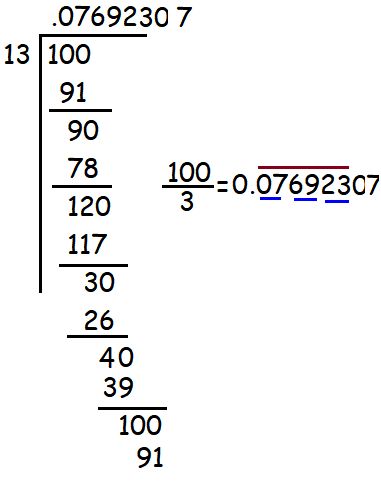
Hence the length of period is 6.

Question 2 :

Express the rational number 1/33 in recurring decimal form by using the recurring decimal expansion of 1/11. Hence write 71/33 in recurring decimal form.

Solution :

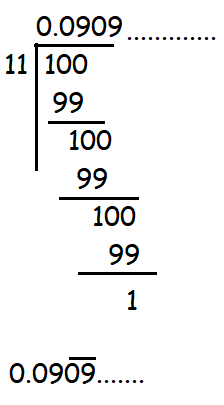
1/11  =  0.0909..........

1/33  =  (1/3) (1/11)  =  (1/3)(0.0909......)

1/33  =  0.0303...........

71/33  =  71(1/33)

=  71(0.03 bar)

=  2.15 bar

How to Express the Decimals as Fractions

Question 3 :

Express the following decimal expression into rational numbers.

(i) 0.24 (bar)

Solution :

Let x  =  0.242424............  -----(1)

Since we have the sign bar for two digits, we have to multiply (1) by 100 on both sides.

100x  =  24.2424...........------(2)

(2) - (1)  

100x - x  =  24.2424......-0.2424...........

99x  =  24

x  =  24/99

x  =  8/33

Hence the rational form of the given decimal is 8/33.

(ii)  2.327 (bar)

Solution :

Let x  =  2.327327............  -----(1)

Since we have the sign bar for three digits, we have to multiply (1) by 1000 on both sides.

1000x  =  2327.327327...........------(2)

(2) - (1)  

1000x - x  =  2327.327327.....-2.327327........

999x  =  2325

x  =  2325/999

x  =  775/333

Hence the rational form of the given decimal is 775/333.

(iii)  -5.132

Solution :

The given decimal is terminating decimal. We have three digits after the decimal. So, we have to multiply the numerator and denominator by 1000.

-5.132  =   -5132/1000

  =  -2566/500

  =  -1283/250

(iv)  3.17 (bar) (bar is only for 7)

Solution :

Let x  =  3.177777...........  -----(1)

Since we have the sign bar for only one digit, we have to multiply (1) by 10 on both sides.

10x  =  31.77777...........------(2)

(2) - (1)  

10x - x  =  31.7777.....-3.17777........

9x  =  28.6

x  =  28.6/9

Multiply both numerator and denominator by 10.

x  =  286/90

x  =  143/45

Hence the fractional form of the given decimal is 143/45.

(v)  17.215 (bar is for 1 and 5)

Solution :

Let x  =  17.2151515...........  -----(1)

Since we have the sign bar for two digits, we have to multiply (1) by 100 on both sides.

100x  =  1721.51515...........------(2)

(2) - (1)  

100x - x  =  1721.51515.......... - 17.2151515...........

99x  =  1704.3

x  =  1704.3/99

Multiply both numerator and denominator by 10.

x  =  17043/990

x  =  5681/330

Hence the fractional form of the given decimal is 5681/330.

(vi)  -21.2137 (bar is for 7)

Solution :

Let x  =  21.213777...........  -----(1)

Since we have the sign bar for two digits, we have to multiply (1) by 100 on both sides.

10x  =  212.137777...........------(2)

(2) - (1)  

10x - x  =  212.137777........... - 21.213777...........

9x  =  191.92

x  =  191.924/9

x  =  190924/9000

x  =  47731/2250

Let see the next concept on "How to Check Which Type of Decimal Expansion".

How to Check if the Fraction has Terminating Decimal ?

Question 4 :

Without actual division, find which of the following rational numbers have terminating decimal expansion.

(i)  7/128

Solution :

128  =  2⁷

7/128  =  7/2⁷

Since the denominator is in the form 2^m x 5ⁿ, the given fraction is terminating decimal.

(ii)  21/15

Solution :

21/15  =  7/5

Since the denominator is not in the form 2^m x 5ⁿ, the given fraction is non terminating decimal.

(iii)  4  9/35

Solution :

4  9/35  =  149/35

35  =  7 x 5

Since the denominator is not in the form 2^m x 5ⁿ, the given fraction is non terminating decimal.

(iv)  219/2200

Solution :

2200  =  5² x 2³ x 11

Since the denominator is in the form 2^m x 5ⁿ, the given fraction is non terminating decimal.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.