HOW TO CONVERT INTERVAL NOTATION TO INEQUALITY

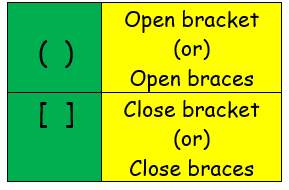
An open interval does not include its endpoints, and is enclosed in parentheses.

A closed interval includes its endpoints, and is enclosed in square brackets.

An interval is considered bounded if both endpoints are real numbers. An interval is unbounded if both endpoints are not real numbers.

Convert interval notation to inequality notation or vice versa. Find the endpoints and state whether the interval is bounded, its type, and graph the interval.

Example 1 :

[-6, 3)

Solution :

From the interval, we find more than one value. Let us consider every value as x.

Converting the given interval into inequality, we get

-6 ≤ x < 3

So, the possible values of x are {-6, -5, -4, -3, ......2}.

By drawing the possible solutions in number line, we get

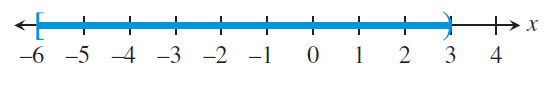
Example 2 :

(-∞, -1)

Solution :

From the interval, we find more than one value. Let us consider every value as x.

Converting the given interval into inequality, we get

-∞ < x < -1

By drawing the possible solutions in number line, we get

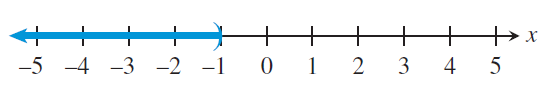
Example 3 :

[-2, 3]

Solution :

From the interval, we find more than one value. Let us consider every value as x.

Converting the given interval into inequality, we get

-2 ≤ x  ≤ 3

By drawing the possible solutions in number line, we get

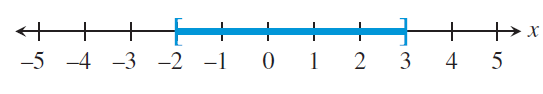
Example 4 :

Use an inequality to describe the interval of real numbers.

(i)  [-1, 1)   (ii)  (-∞, 4]

Solution :

(i) Possible solutions are -1, 0. By writing it using inequality, we get

-1 ≤ x < 1

(ii)  Possible solutions are

...........-1, 0, 1,........4.

By writing it using inequality, we get

-∞ < x ≤ 4

Example 5 :

Use an inequality to describe the interval of real numbers.

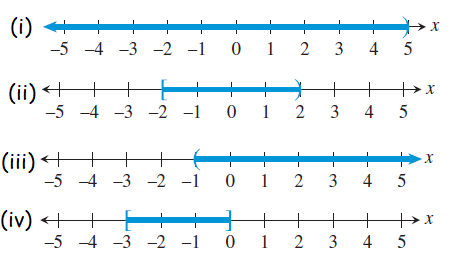
Solution :

Example 6 :

Tom is deciding whether or not he should become a member gym to use their basketball courts. The membership cost is $135.

Members pay $2 to rent out the basketball courts. Non-members can rent the court also, but they have to pay $11 each time. How many times would Tom need to rent the court in order for it be cheaper to be a member than a non member?

Solution :

Let x be the number of times he is using basketball court.

Cost of membership = $135

Non members should pay $11 each time

135 + 2x < 11x

Subtracting 11x one both sides and subtracting 135 on both sides, we get

-9x < -135

Dividing by 9 on both sides

x > 135/9

x > 15

He need to rent more than 15 times.

Example 7 :

Ryan is a wrestler trying to make weight. He currently weighs 200 lbs. If he cuts 2 lbs. per week, how many weeks will it take him to weigh less than 175 lbs.?

Solution :

Ryan's weight = 200 lbs

Every week he cuts = 2 lbs

Let x be the number of weeks

200 - 2x < 175

-2x < 175 - 200

-2x < -25

x > 25/2

x > 12.5

So, he should take more than 12 weeks.

Example 8 :

Allison practices her violin for at least 12 hours per week. She practices for three fourths of an hour each session. If Allison has already practiced 3 hours this week, how many more sessions remain for her to meet or exceed her weekly practice goal?

Solution :

Let x be the number of hours he is doing practice

Duration of each session = 0.75 hours

3 + 0.75x ≥ 12

Since it is atleast 12 hours, we put the greater than sign.

0.75x ≥ 12 - 3

0.75x ≥ 9

x ≥ 9/0.75

x ≥ 12

So, more than 12 sessions to exceed her weekly practice goal.

Example 9 :

Pet Supplies makes a profit of $5.50 per bag on its line of natural dog food. If the store wants to make a profit of no less than $5225, how many bags of dog food does it need to sell?

Solution :

Let x be the number of bags required.

5.50x ≥ 5225

x ≥ 5225/5.50

x ≥ 950

So, more than 950 bags.

Example 10 :

Christ want to order DVD's online. Each DVD cost $11.59 and shipping the entire order costs $9.99. If he can spend no more than $100, how many DVD's can he buy ?

Solution :

Cost of each DVD = 11.59

Amount of shipping = 9.99

Let x be the number of DVD's he can buy.

11.59 x + 9.99 ≤ 100

(no more than 100).

11.59x ≤ 100 - 9.99

11.59x ≤ 90.01

x ≤ 7.76

He can busy less than 7 DVDs.

Example 11 :

A taxi charges a rate of $1.75 plus an additional $0.65 per mile. If Erica has at most $10 to spend on the cab ride, how far could she travel?

Solution :

Let x be the number of additional mile they drive. Maximum amount she can spend is $10.

1.75 + 0.65x < 10

Subtracting 1.75, we get

0.65x < 10 - 1.75

0.65 x < 8.25

x < 8.25/0.65

x < 12.6

Less than 12 miles she can travel to spend the amount lesser than $10.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.