HOW TO DETERMINE WHETHER THE GRAPH IS A FUNCTION

Example 1  :

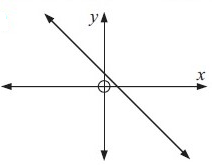
Solution :

Drawing a vertical lines across the graph, we get

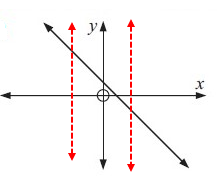
Each vertical lines are intersecting the graph at most once. So, the given graph represents the function.

Example 2 :

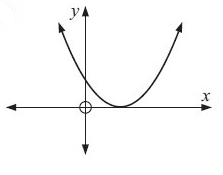
Solution :

Drawing a vertical lines across the graph, we get

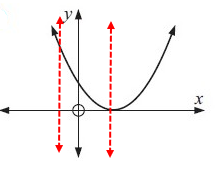
Each vertical lines are intersecting the graph at most once. So, the given graph represents the function.

Example 3 :

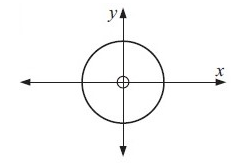
Solution :

Drawing a vertical lines across the graph, we get

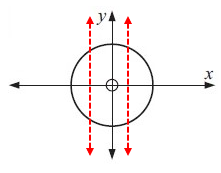
Each vertical line is intersecting the graph at more than one point. So, it is not a function.

Example 4 :

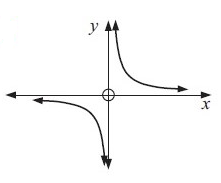
Solution :

Drawing a vertical lines across the graph, we get

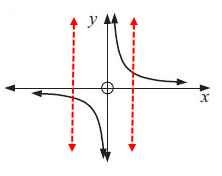
Every vertical line is intersecting the graph at most once. So, the given graph represents the function.

Example 5 :

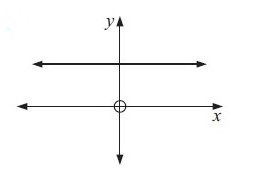
Solution :

Drawing a vertical lines across the graph, we get

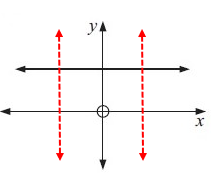
Each vertical line is intersecting the graph at most once. So, the given graph represents the function.

Example 6 :

Use the vertical line test to determine whether the following graph represents a function.

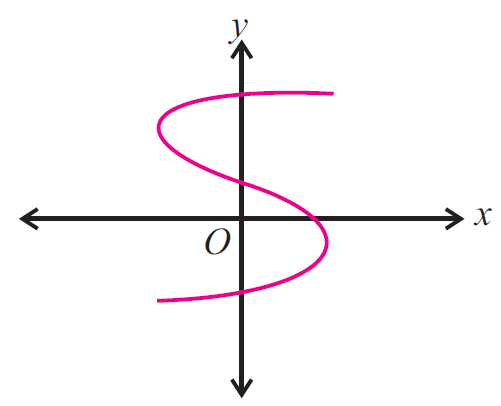
Solution :

Drawing a vertical lines across the graph, we get

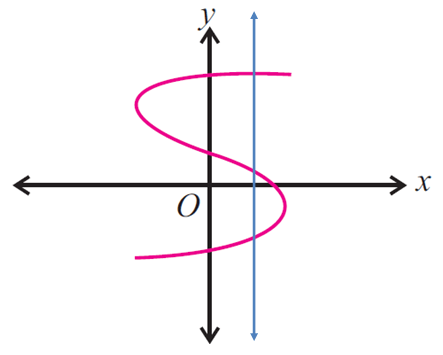
In the above graph, the vertical line intersects the graph in more than one point (three points), then the given graph does not represent a function. 

Example 7 :

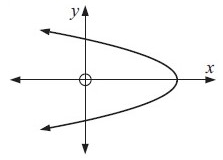
Solution :

Drawing a vertical lines across the graph, we get

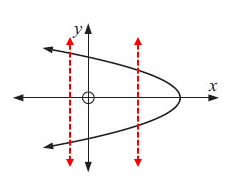
In the above graph, the vertical line intersects the graph in more than one point (two points), then the given graph does not represent a function. 

Example 8 :

Rewrite the relation given in the scatter plot as a mapping diagram.

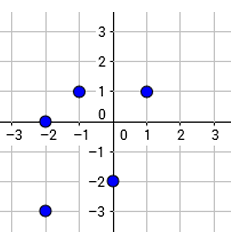
Is this relation also a function ?

Solution :

Points shown in the coordinate plane are

(1, 1) (-1, 1) (-2, 0) (0, -2) and (-2, -3)

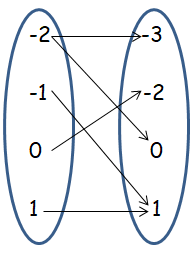
Here the input -2 is associated with more than one output. So, this relation is not a function.

Example 9 :

Rewrite the relation given in the scatter plot as a set of ordered pairs.

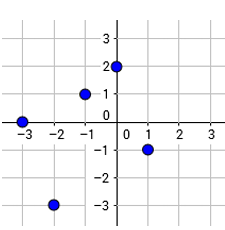
is this relation a function ?

Solution :

Writing the points from the coordinate plane.

(0, 2) (-1, 1) (1, -1) (-3, 0) (-2, -3)

Since each input is associated with different outputs, this relation is a function.

Example 10 :

Determine if each graph shows a function or a relation only. Then identify the domain and range.

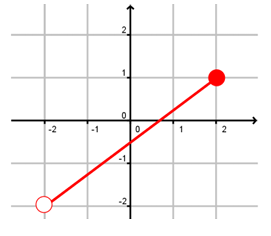
Solution :

By drawing the vertical line, it is intersecting the graph maximum once. So, this relation is a function.

By observing the graph horizontally, the possible inputs is domain.

Domain = -2 < x ≤ 2

By observing the graph vertically, the possible outputs is domain.

Range = -2 < x ≤ 1

Example 11 :

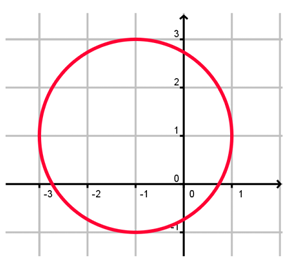
Solution :

By drawing the vertical line, it is not intersecting the graph maximum once. So, this relation is not a function.

By observing the graph horizontally, the possible inputs is domain.

Domain = -3 ≤ x ≤ 1

By observing the graph vertically, the possible outputs is domain.

Range = -1 ≤ x ≤ 3

Example 12 :

Identify the domain and range, then evaluate each function for the given value of x.

f = {(10, 7) (-2, 4) (5, 3) (4, 10)}

i)   Domain     ii)  Range     iii) f(5)

Solution :

f = {(10, 7) (-2, 4) (5, 3) (4, 10)}

i)

Possible inputs are domain.

Domain = {-2, 4, 5, 10}

ii)

Outputs are range.

Range = {3, 4, 7, 10}

iii) f(5) = 3

Example 13 :

Identify the domain and range, then evaluate each function for the given value of x.

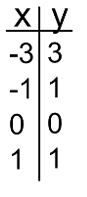
i)   Domain     ii)  Range     iii) f(1)

Solution :

f = {(-3, 3) (-1, 1) (0, 0) (1, 1)}

i) Domain = {-3, -1, 0, 1}

ii) Range = {0, 1, 3}

iii) f(1) = 1

Example 14 :

Identify the domain and range, then evaluate each function for the given value of x.

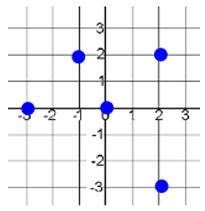
i)   Domain     ii)  Range     iii) f(-3)

Solution :

f = {(2, 2) (0, 0) (-1, 2) (-3, 0) (2, -3)}

i) Domain = {-3, -1, 0, 2}

ii) Range = {-3, 0, 2}

iii) f(-3) = 0

Example 15 :

Using the vertical line test, determine if the graph above shows a relation, a function, both a relation and a function, or neither a relation nor a function.

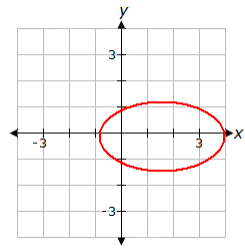
A. neither a relation nor a function

B. relation only

C. both a relation and a function

D. function only

Solution :

The vertical line will intersect the graph more than one point. So, it is not a function. It is relation only. So, option B is correct.

Example 16 :

Which of the following relations describes a function?

A. { (0, 0), (0, 2), (2, 0), (2, 2) }

B. { (2, 2), (2, 3), (3, 2), (3, 3) }

C. { (2, -1), (2, 1), (3, -1), (3, 1) }

D. { (-2, -3), (-3, -2), (2, 3), (3, 2) }

Solution :

Option A :

{ (0, 0), (0, 2), (2, 0), (2, 2) }

The input 0 is having more than one output 0 and 2. So, it is not a function.

Option B :

{ (2, 2), (2, 3), (3, 2), (3, 3) }

The input 2 is having more than one output 2 and 3. So, it is not a function.

Option C :

{ (2, -1), (2, 1), (3, -1), (3, 1) }

The input 2 is having more than one output -1 and 1. So, it is not a function.

Option D :

{ (-2, -3), (-3, -2), (2, 3), (3, 2) }

Each input is having maximum one output. So, this relation represents a function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.