HOW TO EVALUATE LIMITS FROM A GRAPH
Let f be a function of a real variable x. Let a, L be two fixed real values. When x approaches the real value a, f(x) approaches the real value L, we say L is the limit of the function f(x) as x tends to a.
This is written as
lim f(x) = L
x--> a
Here, we may have a question. When x approachs a, whether x approaches a from its left side or right side.
If x approaches a from its left side, it is called left-sided limit and if x approaches a from its right side, it is called right sided limit.
Left-Sided Limit
For example, let x approach 0 from its left side. Then, x will take the values which are very close to zero, finally it will reach 0 as shown in the picture below.

In the graph shown below, when x approaches a real value a from its left side, f(x) approaches the real value L.
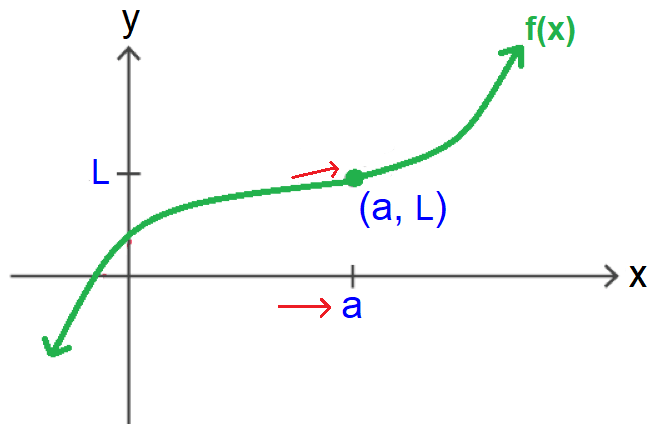
Therefore, L is the left sided limit of the function f(x) as x tends to a.
This is written as
lim f(x) = L
x--> a-
In the above limit, to indicate the left-sided limit, there is a negative sign on the right top corner of a.
Right-Sided Limit
Let x approach 0 from its right side. Then, x will take the values which are very close to zero, finally it will reach 0 as shown in the picture below.
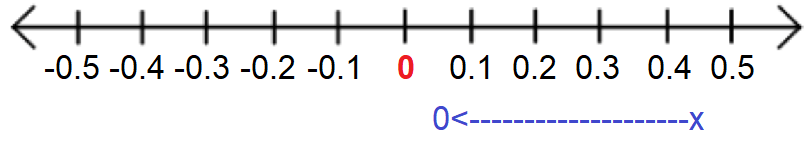
In the graph shown below, when x approaches a real value a from its right side, f(x) approaches the real value L.
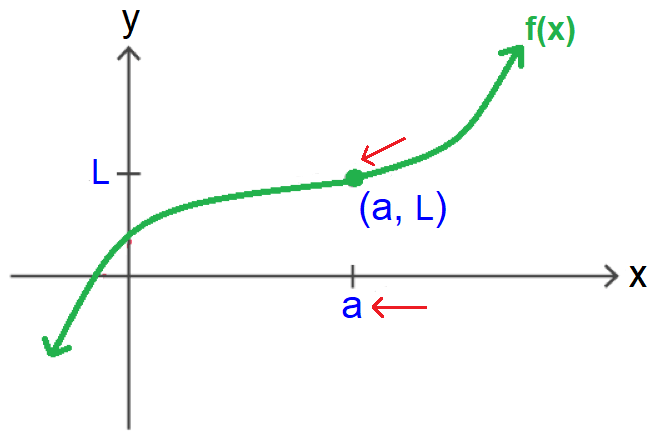
Therefore, L is the right sided limit of the function f(x) as x tends to a.
This is written as
lim f(x) = L
x--> a+
In the above limit, to indicate the right-sided limit, there is a positive sign on the right top corner of a.
Two-Sided Limit
Consider the left-sided limit and right sided limit are shown below.
lim f(x) = L
x--> a-
lim f(x) = L
x--> a+
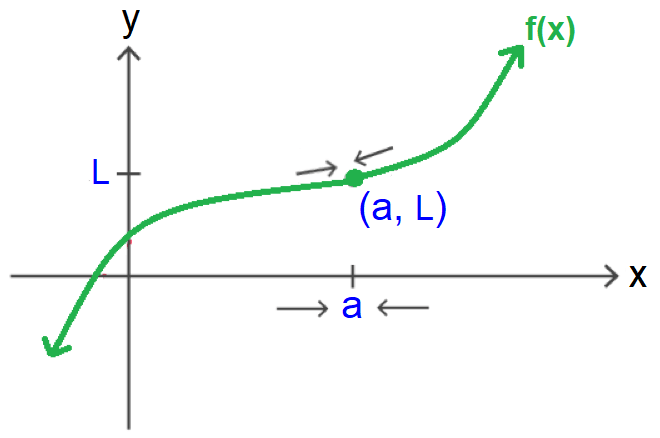
When x approaches the real value a from both its left side and right side, f(x) approaches the same real value L in both the cases. Therefore, L is the two sided limit of the function f(x) as x tends to a.
This is written as
lim f(x) = L
x--> a
When we write two-sided limit, there won't be any sign on the right top corner of a.
It has been illustrated in the graph shown below.
What if the left-sided limit and right-sided limit are not equal?
Consider the graph shown below.
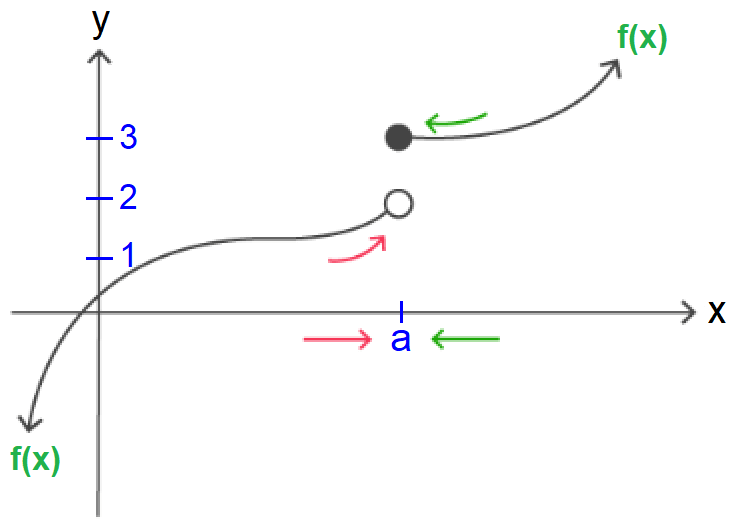
In the graph shown above, when x approaches the real value a from its left side, f(x) approaches the real value 2.
lim f(x) = 2
x--> a-
When x approaches the real value a from its right side, f(x) approaches the real value 3.
lim f(x) = 3
x--> a+
So, the left-sided limit of f(x) and the right sided limit of f(x) are not equal, as x approches a.
lim f(x) ≠ lim f(x)
x--> a- x--> a+
If left-sided limit and right-sided limit are not equal, then the two-sided limit does not exist.
That is,
lim f(x) does not exist
x--> a
Solved Examples
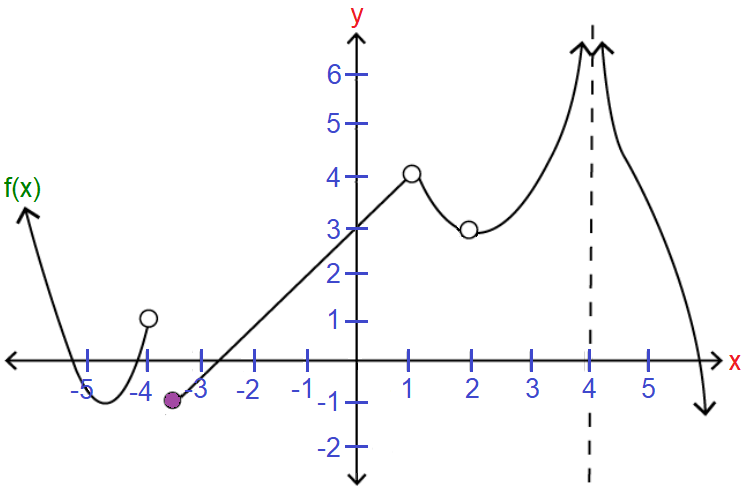
From the graph shown above, evaluate each of the following limits.
Example 1 :
lim f(x)
x--> -4-
Solution :
We have to evaluate left-sided limit of f(x) as x approaches -4.
In the graph shown above, when x approches -4 from its left side, f(x) approaches 1.
Therefore,
lim f(x) = 1
x--> -4-
Example 2 :
lim f(x)
x--> -4+
Solution :
We have to evaluate right-sided limit of f(x) as x approaches -4.
In the graph shown above, when x approches -4 from its right side, f(x) approaches -1.
Therefore,
lim f(x) = -1
x--> -4-
Example 3 :
lim f(x)
x--> -4
Solution :
We have to evaluate two-sided limit of f(x) as x approaches -4.
From the solutions of Examples 1 and 2 above,
|
lim f(x) = 1 |
lim f(x) = -1 |
lim f(x) ≠ lim f(x)
x--> -4- x--> -4+
Since, the left-sided limit and right sided limit are not equal, two-sided limit does not exist.
That is,
lim f(x) does not exist
x--> -4
Example 4 :
lim f(x)
x--> 1-
Solution :
We have to evaluate left-sided limit of f(x) as x approaches 1.
In the graph shown above, when x approches 1 from its left side, f(x) approaches 4.
Therefore,
lim f(x) = 4
x--> 1-
Example 5 :
lim f(x)
x--> 1+
Solution :
We have to evaluate right-sided limit of f(x) as x approaches 1.
In the graph shown above, when x approches 1 from its right side, f(x) approaches 4.
Therefore,
lim f(x) = 4
x--> 1+
Example 6 :
lim f(x)
x--> 1
Solution :
We have to evaluate two-sided limit of f(x) as x approaches 1.
From the solutions of Examples 4 and 5 above,
|
lim f(x) = 4 |
lim f(x) = 4 |
lim f(x) = lim f(x)
x--> 1- x--> 1+
Since, the left-sided limit and right sided limit are equal, two-sided limit exists.
That is,
lim f(x) = 4
x--> 1
Example 7 :
lim f(x)
x--> 2-
Solution :
We have to evaluate left-sided limit of f(x) as x approaches 2.
In the graph shown above, when x approches 2 from its left side, f(x) approaches 3.
Therefore,
Therefore,
lim f(x) = 3
x--> 2-
Example 8 :
lim f(x)
x--> 2+
Solution :
We have to evaluate right-sided limit of f(x) as x approaches 2.
In the graph shown above, when x approches 2 from its right side, f(x) approaches 3.
Therefore,
lim f(x) = 3
x--> 2+
Example 9 :
lim f(x)
x--> 2
Solution :
We have to evaluate two-sided limit of f(x) as x approaches 2.
From the solutions of Examples 7 and 8 above,
|
lim f(x) = 3 |
lim f(x) = 3 |
lim f(x) = lim f(x)
x--> 2- x--> 2+
Since, the left-sided limit and right sided limit are equal, two-sided limit exists.
That is,
lim f(x) = 3
x--> 2
Example 10 :
lim f(x)
x--> 4-
Solution :
We have to evaluate left-sided limit of f(x) as x approaches 4.
In the graph shown above, when x approches 4 from its left side, f(x) approaches +∞.
Therefore,
lim f(x) = +∞
x--> 4-
Example 11 :
lim f(x)
x--> 4+
Solution :
We have to evaluate right-sided limit of f(x) as x approaches 4.
In the graph shown above, when x approches 4 from its right side, f(x) approaches +∞.
Therefore,
lim f(x) = +∞
x--> 4+
Example 12 :
lim f(x)
x--> 4
Solution :
We have to evaluate two-sided limit of f(x) as x approaches 4.
From the solutions of Examples 10 and 11 above,
|
lim f(x) = +∞ |
lim f(x) = +∞ |
lim f(x) = lim f(x)
x--> 4- x--> 4+
Since, the left-sided limit and right sided limit are equal, two-sided limit exists.
That is,
lim f(x) = +∞
x--> 4
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144)

