HOW TO EXPRESS THE GIVEN MATRIX AS SUM OF SYMMETRIC AND SKEW SYMMETRIC

What is symmetric and skew symmetric matrix ?

For any square matrix A with real number entries, A+ A^T is a symmetric matrix and A− A^T is a skew-symmetric matrix.

Any square matrix can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix.

Let A be a square matrix. Then, we can write

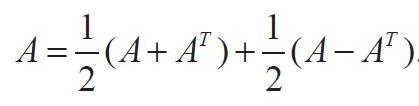
Let us look into some problems to understand the concept.

Question 1 :

Express the following matrices as the sum of a symmetric matrix and a skew-symmetric matrix:

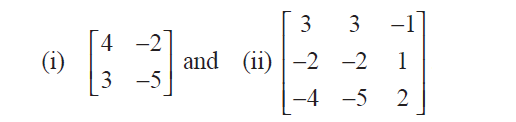
Solution :

First let us add the matrices A and A^T, then we have to multiply it by 1/2

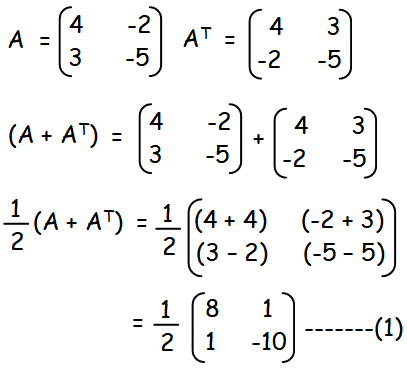
Now we have to subtract the matrices A and A^T, then we have to multiply it by 1/2

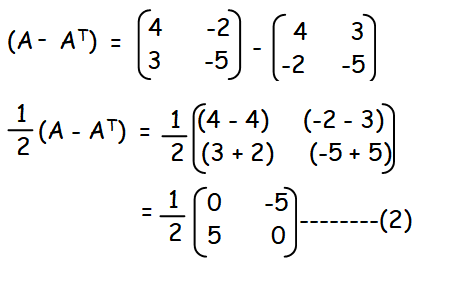
By adding the above two matrices, we get the original question.

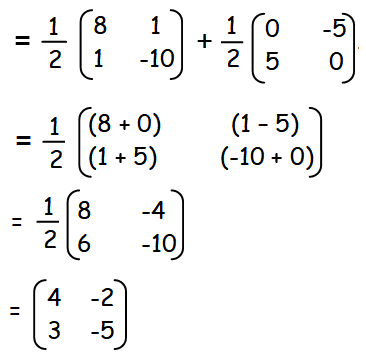
Hence proved.

(ii)  From the given matrix A, we have to find A^T

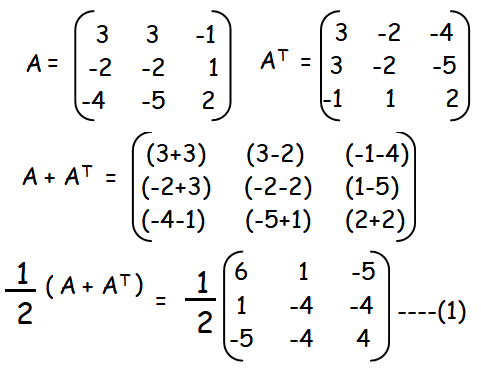
So far we get symmetric matrix. Now we are going to find skew symmetric matrix.

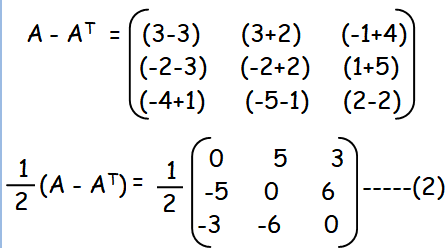
By adding (1) and (2), we get

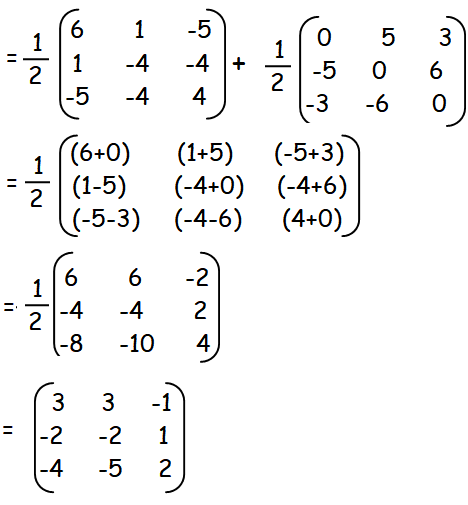
Hence proved.

Question 3 :

Find the matrix A such that

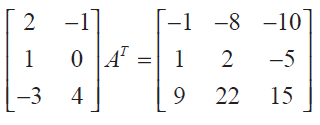
Solution :

Let the required matrix A^T be

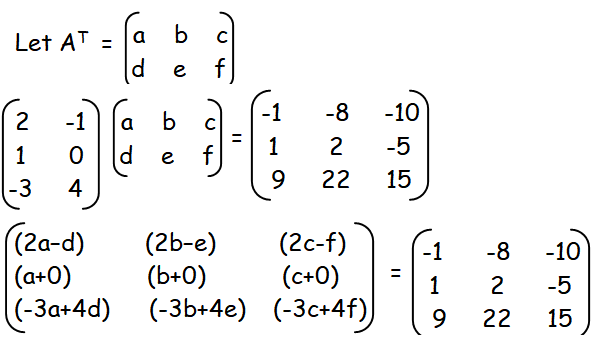
By equating the corresponding terms, we get

2a-d  =  -1  ----(1)

2b - e  = -8 ----(2)

2c - f  =  -10 ----(3)

a  =  1, b  =  2  and c  =  -5

By applying the value of a in the first equation, we get the value d.

2(1) - d  =  -1

 2 - d  =  -1

-d  =  -1 - 2

-d  =  -3

d  =  3

By applying the value of b in the second equation, we get the value e.

2(2) - e  = -8

 4 - e  =  -8

-e  =  -8 - 4

-e  =  -12

e  =  12

By applying the value of c in the third equation, we get the value f.

2(-5) - f  =  -10

 -10 - f  =  -10

-f  =  -10 + 10

f  =  0

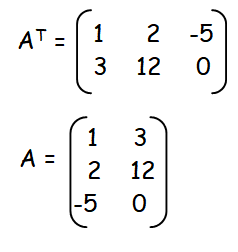
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.