HOW TO FACTOR TRINOMIALS WITH 2 DIFFERENT VARIABLES

Grouping means factoring out the common stuff found in all the given terms. 

Factoring polynomials can be done by the following methods

(i) Factoring by grouping.

(ii) Factoring using algebraic identities.

Factoring by Grouping

Example 1 :

Factor : 

pq - pr - 3ps

Solution :

=  pq - pr - 3ps

We find 'p' in all the terms. So, 'p' can be factored out as shown below.  

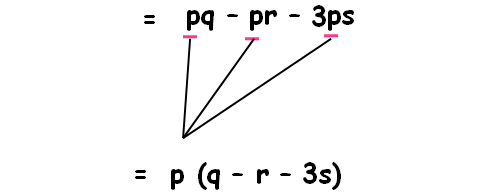
Example 2 :

Factor : 

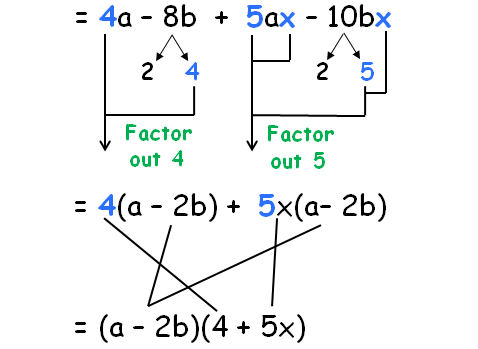
4a - 8b + 5ax - 10bx

Solution :

=  4a - 8b + 5ax - 10bx

We can group the terms in the above expression as shown below. 

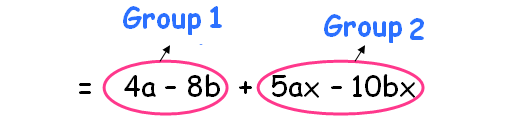
We find 4 in common the terms of the first group. So, 4 can be factored out. 

We find 5x in common the terms of the second group. So,  5x can be factored out. 

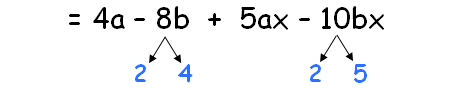
Factor out the common stuff. 

Example 3 :

Factor : 

2a³ - 3a²b + 2a²c

Solution :

=  2a³ - 3a²b + 2a²c

In the given expression, we a² in common. So, a² can be factored out.  

=  a²(2a - 3b + 2c)

So, 

4a - 8b + 5ax - 10bx  =  a²(2a - 3b + 2c)

Example 4 :

Factor : 

10x³ - 25x⁴ y

Solution :

=  10x³ - 25x⁴ y

We find 5x³ in common in the given terms. So, 5x³ can be factored out.   

=  5x³(2 - 5xy)

Factoring using Algebraic Identities

Example 1 :

Factorize : 

x² + 12y + 36y²

Solution :

=  x² + 2(x)(6y) + (6y)²

The above expression is in the form 'a² - 2ab + b²'. We know that 

a² - 2ab + b²  =  (a + b)²

Then, 

=  (x + 6y)²

Example 2 :

Factorize : 

9x² - 24xy + 16y²

Solution :

=  9x² - 24xy + 16y²

=  (3x)² - 2(3x)(4y) + (4y)²

The above expression is in the form 'a² - 2ab + b²'. We know that 

a² - 2ab + b²  =  (a - b)²

Then, 

=  (3x - 4y)²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.