HOW TO FIND A LIMIT USING A TABLE
Here we are going to see how to find a limit using a table.
First let us understand what is limit.
Let I be an open interval containing x0 ∈ R.
Let f : I ---> R. Then we say that the limit of f(x) is L, as x approaches x0 [Usually written as limx--->0f(x) = L]. Whenever x becomes sufficiently close to x0 from either side with x ≠ x0, f(x) gets sufficiently close to L.
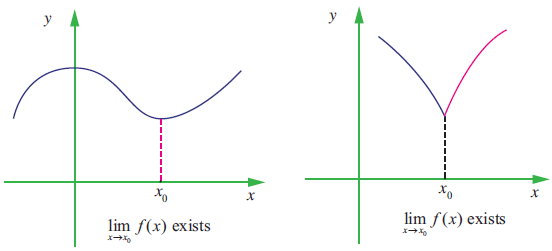
In the following examples, complete the table using calculator and use the result to estimate the limit.
Example 1 :
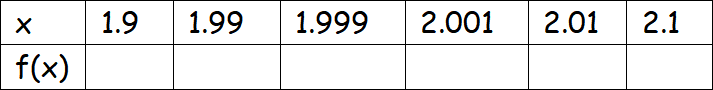
Solution :
Substitute the values of x from the table above into f(x).
When x = 1.9,
When x = 1.99,
When x = 1.999,
When x = 2.001,
When x = 2.01,
When x = 2.1,
From the above table, we have to estimate the limit when x tends to 2.
Here x--->2 appears between 1.999 to 2.001. By observing the table, we may estimate the limit as 0.333.....
Example 2 :
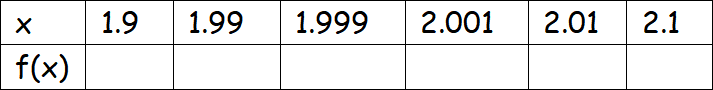
Solution :
Substitute the values of x from the table above into f(x).
When x = 1.9,
When x = 1.99,
When x = 1.999,
When x = 2.001,
When x = 2.01,
When x = 2.1,
Here x--->2 appears between 1.999 to 2.001. By observing the table, we may estimate the limit as 0.25.
Example 3 :
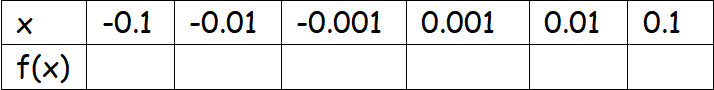
Solution :
When x = -0.1,
When x = -0.01,
When x = -0.001,
When x = 0.001,
When x = 0.01,
When x = 0.1,
Here x--->0 appears between -0.001 to 0.001. By observing the table, we may estimate the limit as 0.288.....
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 21, 24 02:20 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 90)
Dec 21, 24 02:19 AM
Digital SAT Math Problems and Solutions (Part - 90) -
Digital SAT Math Problems and Solutions (Part - 89)
Dec 20, 24 06:23 AM
Digital SAT Math Problems and Solutions (Part - 89)
