HOW TO FIND AREA OF TRIANGLE WHEN EQUATION OF SIDES ARE GIVEN

Question :

Find the area of a triangle formed by the lines

3x + y − 2  =  0

5x + 2y − 3  =  0

2x − y − 3  =  0

Answer :

3x + y − 2 = 0  ------(1)

5x + 2y − 3 = 0  ------(2)

2x − y − 3 = 0  ------(3)

Point of intersection of (1) and (2) is the vertex A

Point of intersection of (2) and (3) is the vertex B

Point of intersection of (3) and (1) is the vertex C

2(1) - (2) : 

x - 1  =  0

Substitute 1 for x in (1).

(1)-----> 3(1) + y - 2  =  0

1 + y  =  0

y  =  -1

Vertex A(1, -1).

(2) + 2(3) :

9x - 9  =  0

9x  =  9

x  =  1

Substitute 1 for x in (2).

(2)-----> 5(1) + 2y - 3  =  0 

5 + 2y - 3  =  0

2y + 2  =  0

2y  =  -2

y  =  -1

Vertex B (1, -1)

(1) + (3) :

5x - 5  =  0

x  =  1

Substitute 1 for x (3).

(1)-----> 2(1) - y - 3  =  0

2 - y - 3  =  0

- y - 1  =  0

-y  =  1

y  =  -1

Vertex C(1, -1). 

Vertices of the triangle are 

A(1, -1) B(1, -1) and C(1, -1)

Now, let us find the area of triangle using the above vertices.

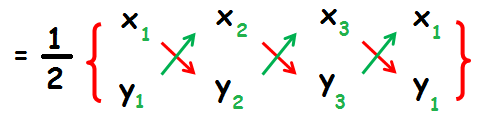
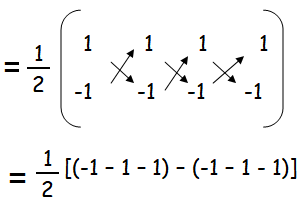
  =  (1/2)[(-3 +3)]

  =  0 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.