HOW TO FIND CENTER AND RADIUS FROM AN EQUATION IN COMPLEX NUMBERS

How to Find Center and Radius From an Equation in Complex Numbers :

Here we are going to see some example problems based on finding center and radius from an equation in complex numbers.

How to Find Center and Radius From an Equation in Complex Numbers

Equation of the Circle from Complex Numbers

The locus of z that satisfies the equation |z − z₀| = r where z₀ is a fixed complex number and r is a fixed positive real number consists of all points z whose distance from z₀ is r .

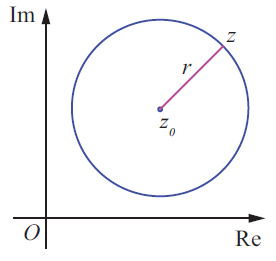
So, |z − z₀| = r is the complex form of the equation of a circle.

(i) |z − z₀| < r represents the points interior of the circle.

(ii) |z − z₀| > r represents the points exterior of the circle.

Note :

|z| = r ==> √x² + y²  =  r

x² + y²  =  r², represents a circle centre at the origin with radius r units.

Finding Centre and Radius of Circle From Complex Numbers  - Examples

Question 1 :

Show that the following equations represent a circle, and, find its centre and radius

(i)  |z - 2 - i|  =  3

Solution :

|z - 2 - i|  =  3

|z - (2 + i)|  =  3

It is of the form |z − z₀| = r and so it represents a circle, whose centre and radius are (2, 1) and 3 respectively.

(ii) |2z + 2 − 4i| = 2

Solution :

|2z + 2 − 4i| = 2

2|z + (2 − 4i)/2| = 2

|z + (2 − 4i)/2| = 1

|z - (-(1 - 2i))| = 1

|z - (-1 + 2i)| = 1

It is of the form |z − z₀| = r and so it represents a circle, whose centre and radius are (-1, 2) and 1 respectively. 

(iii) |3z − 6 +12i|  =  8.

Solution :

|3z − 6 +12i|  =  8

3|z - (6 − 12i)/3| = 8

|z - (2 − 4i)| = 8/3

It is of the form |z − z₀| = r and so it represents a circle, whose centre and radius are (2, -4) and 8/3 respectively. 

After having gone through the stuff given above, we hope that the students would have understood, "How to Find Center and Radius From an Equation in Complex Numbers". 

Apart from the stuff given in this section "How to Find Center and Radius From an Equation in Complex Numbers", if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.