HOW TO FIND CENTROID OF A TRIANGLE WITH COORDINATES

The centroid of a triangle is the point of concurrency of the medians.

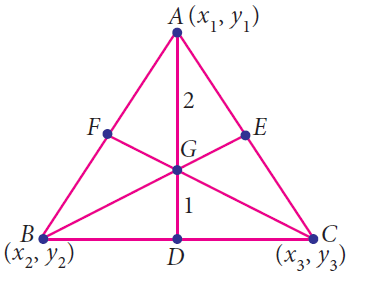
In the above triangle , AD, BE and CF are called medians. All the three medians AD, BE and CF are intersecting at G. So  G is called centroid of the triangle

If the coordinates of A, B and C are (x_1, y₁), (x_2, ,y₂) and (x₃, y₃), then the formula to determine the centroid of the triangle is given by

Example 1 :

Find the centroid of a triangle whose vertices are the points (6, -1), (8, 3) and (10, -5).

Solution :

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  6, x₂  =  8 and x₃  =  10

y₁  =  -1, y₂  =  3 and y₃  =  -5

Then, 

=  [(6 + 8 + 10)/3, (-1 + 3 - 5)/3]

=  (24/3, -3/3)

=  (8, -1)

So, the centroid of the given triangle is (8, -1). 

Example 2 :

Triangle ABC has vertices as shown.

Find 

(a)  the coordinates of P, Q and R, the midpoints of AB, BC and AC respectively.

(b)  The equation of the perpendicular bisector of 

(i)  AB  (ii)  BC  (iii)  CA

(c)   The coordinates of X, the point of intersection of perpendicular bisector of AB and perpendicular bisector BC.

(d)  Does the point X lie on the perpendicular bisector of AC ?

(e)  What is special about the point X in relation to the vertices of the triangle ABC.

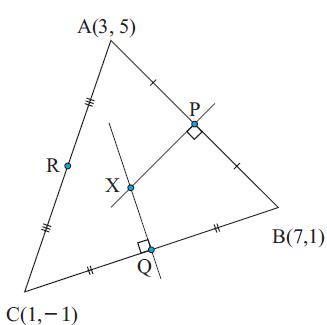
Solution :

(a)  Midpoint of the line segment joining two points

A(3, 5) and B(7, 1).

P  =  Midpoint of AB  =  [(x₁ + x₂)/2, (y₁ + y₂)/2]

Midpoint of AB  =  (3+7)/2, (5+1)/2

P  =  (5, 3)

So, the coordinates of P(5, 3).

Q is the midpoint of two points B(7, 1) and C(1, - 1)

Midpoint of BC  =  [(7+1)/2, (1-1)/2]

Q  =  (4, 0)

So, the coordinates of Q(4, 0)

R is the midpoint of line segment joining the two points A(3, 5) and C(1, - 1).

Midpoint of AC  =  [(3+1)/2, (5-1)/2]

R  =  (2, 2)

So, the coordinates of R(2, 2)

(b)  The equation of the perpendicular bisector of AB

Midpoint of AB  =  (5, 3)

Slope of AB :

m  =  (y₂ – y₁)/(x₂ – x₁)

m₁  =  (1 - 5)/(7 – 3)

m  =  - 4/4

m  =  - 1

Slope of perpendicular bisector PX  =  1

Equation of perpendicular bisector PX  :

y – y₁  =  m (x – x₁)

y-3  =  1(x-5 )

y-3  =  x-5

x–y  =  2

Equation of perpendicular bisector PX is x–y-2  =  0.

Slope of BC :

m  =  (- 1-1)/(1–7)

m  =   2/6

m  =  1/3

Slope of perpendicular bisector QX  =  -3

Equation of perpendicular bisector QX :

y–0  =  - 3(x–4)

y  =  - 3x+12

3x + y  =  12

So, the required equation QX is 3x+y  =  12.

Midpoint of AC  =  (2, 2)

Slope of AC :

m  =  (- 1 - 5)/(1 – 3)

m  =  6/2

m  =  3

Slope of perpendicular bisector RX  =  -1/3

Equation of perpendicular bisector RX :

y–y₁  =  m (x–x₁)

y-2  =  (-1/3) (x–2)

3y-6  =  -x+2

x+3y  =  2+6

x+3y  =  8

So, the required equation RX is x+3y  =  8

(c)  Solving

x–y  =  2 ------(1)

3x+y  =  12 ------(2)

(1) + (2)

4x  =  14

x  =  7/2

By applying the value of x in (1), we get

7/2 - y  =  2

(7/2)-2  =  y

y  =  3/2

(d)  To check if X lies on RX, we will apply x = 7/2 and y = 3/2 in x+3y  =  8

7/2 + 3(3/2)  =  8

7/2+9/2 =  8

16/2  =  8

8  =  8

Since the point satisfies the equation of the line, we decide X is on RX.

(e)  Since X is the point of intersections of median, it is centroid of the triangle.

Example 3 :

Find the third vertex of triangle, if its two vertices are (–4, 1) and (5, 2) and its centroid is (1, 3).

Solution :

Let (x, y) be the third vertex of triangle.

Centroid is at (1, 3)

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

 [(-4 + 5 + x)/3, (1 + 2 + y)/3] = (1, 3)

 (1 + x)/3, (3 + y)/3 = (1, 3)

Equating the x and y-coordinates, we get

(1 + x)/3 = 1 and (3 + y)/3 = 3

1 + x = 3 and 3 + y = 9

x = 3 - 1, y = 9 - 3

x = 2, y = 6

So, the required vertex is at (2, 6).

Example 4 :

The coordinates of the vertices of a triangle are (4, -2 ), (10, 7) and (5, 3). Find the coordinate of Centroid of the triangle.

Solution :

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

= (4 + 10 + 5)/3, (-2 + 7 + 3)/3

= (19/3, 8/3)

So, the required centroid is at (19/3, 8/3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.