HOW TO FIND DOMAIN AND RANGE OF A FUNCTION

Domain : 

Let y  =  f(x) be a function.

Domain is all real values of x for which y is defined.

If there is any value of x for which y is undefined, we have to exclude that particular value from the set of domain. 

Range :  

Let y  =  f(x) be a function.

Range is all real values of y for the given domain (real values of x). 

Let us look at some practice questions to understand how to find domain and range of a function. 

Practice Questions

Question 1 :

Find the domain of 1 / (1 − 2sinx)

Solution :

1 − 2sin x  =  0

- 2sin x  =  - 1

sin x  =  1/2

sin x  =  sin π/6

Since it sin function, the domain will be R - {nπ + (-1)ⁿ π/6}, n ∈ Z

Question 2 :

Find the largest possible domain of the real valued function f(x)  =  √(4 - x²)/ √(x² - 9)

Solution :

Let us equate numerator and denominator equal to 0.

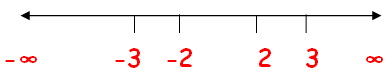
(-∞, -3) (-3, -2) (-2, 2) (2, 3) (3, ∞)

If x ∈ (-∞, -3)

f(-3.5)  =  √(4 - (-3.5)²)/ √((-3.5)² - 9)

  =  √(4 -12.25)/ √(12.25 - 9)

  =  √(-8.25)/ √3.25

  =  Not defined

Hence x ∉ (-∞, -3)

If x ∈ (-3, -2)

f(-2.5)  =  √(4 - (-2.5)²)/ √((-2.5)² - 9)

  =  √(4 -6.25)/ √(6.25- 9)

  =  Not defined

Hence x ∉ (-3, -2)

If x ∈ (-2, 2)

f(0)  =  √(4 - 0²)/ √((0)² - 9)

  =  √4/ √(-9)

  =  Not defined

Hence x ∉ (-2, 2)

If x ∈ (2, 3)

f(2.5)  =  √(4 - (2.5)²)/ √((2.5)² - 9)

  =  √(4 - 6.25)/ √(6.25-9)

  =  Not defined

Hence x ∉ (2, 3)

If x ∈ (3, ∞)

f(4)  =  √(4 - 4²)/ √(4)² - 9)

  =  √(4 - 16)/ √(16-9

  =  Not defined

Hence x ∉ (3, ∞).

Hence the answer is null set.

Question 3 :

Find the range of the function

1 / (2 cos x − 1)

Solution :

Range for cos function is between -1 and 1

-1 ≤ cos x ≤ 1

-2 ≤ 2cos x ≤ 2

-2 - 1 ≤ 2cos x - 1 ≤ 2 - 1

-3 ≤ 2cos x - 1 ≤ 1

Take reciprocal through out the equation, we get

-1/3 ≤ 1/(2cos x - 1) ≤ 1/1

-1/3 ≤ 1/(2cos x - 1) ≤ 1

 (-∞, -1/3] U [1, ∞) is the required range.

Question 4 :

Show that the relation xy = −2 is a function for a suitable domain. Find the domain and the range of the function.

Solution :

xy = −2

y = -2/x

Domain means set of possible values of x.

Domain is all real values expect 0.

Domain  =  R - {0}

x = -2/y

Range means set of possible values of y.

Range is all real values expect 0.

Range  =  R - {0}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.