HOW TO FIND DOMIAN OF A RADICAL FUNCTION

For what values x are the following expressions defined  and find domain.

Example 1 :

√(x-2)

Solution :

y = √(x-2)

Let f(x)  =  (x-2)

Here, radicand x-2 is defined by non-negative number.

x – 2 ≥ 0

Add 2 on both sides, we get

x – 2 + 2 ≥ 0 + 2

x ≥ 2

So, the possible value of x is

x ≥ 2

The function is defined for x ≥ 2.

So, the required domain is [2, ∞).

Example 2 :

√(3–2x)

Solution :

y  =  √(3–2x)

f(x)  =  (3–2x)

Here, radicand  3–2x is defined by non-negative number.

So, domain f(x)  ≥  0

3–2x ≥ 0

Subtract 3 on both sides, we get

3–2x-3 ≥ 0–3

-2x ≥ -3

Dividing by -2 on both sides, change the inequality ≥ into ≤

x ≤ 3/2

So, the possible value of x is

x ≤ 3/2

The function is defined for x ≤ 3/2.

So, the required domain is (-∞, 3/2].

Example 3 :

1/(x+2)

Solution :

y  =  1/(x+2)

Let f(x)  =  √(x+2)

Here, radicand x + 2 in the denominator is defined for all positive values except 0.

To find domain, we can use f(x) > 0.

x+2 > 0

Subtract 2 on both sides, we get

x+2-2 > 0–2

x > -2

So, the possible value of x is

x > -2

The function is defined for x > -2

So, the required domain is (-2, ∞).

Example 4 :

1/√(5+2x)

Solution :

Let f(x)  =  1/√(5+2x)

Here, radicand 5+2x in the denominator is defined by non-negative number.

To find domain, we can use f(x) > 0.

5 + 2x > 0

Subtract 5 on both sides, we get

5 + 2x - 5 > 0 – 5

2x > -5

Dividing by 2 on both sides, we get

x > -5/2

The possible value of x is x > -5/2

So, the domain is (-5/2, ∞).

Example 5 :

√[x(x – 2)]

Solution :

Let f(x)  =  √[x(x – 2)]

Here, radicand  x(x – 2) is defined by non-negative numbers.

So set that expressions,

x(x – 2) ≥ 0

x  =  0 and x – 2  =  0

Now, we have to choose only positive.

So the possible values of x are

x ≤ 0 or x ≥ 2

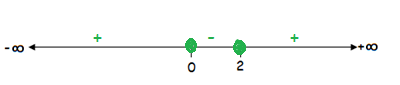
The Domain is (-∞, 0] u [2, ∞)

Example 6 :

(1/√x) + (1/√(2 – x))

Solution :

y  =  (1/√x) + (1/√(2 – x))

Here, radicand x and 2 – x in the denominators is defined by the non-negative numbers.

So set that expressions,

x > 0

2 – x > 0

Subtract  2 on both sides, we get

2 – x – 2 > 0 – 2

- x > - 2

x < 2

Now, we have to choose only positive.

So, the possible values of x are

0 < x < 2

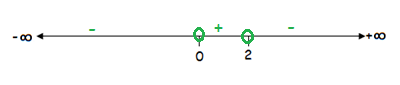
The domain is (0, 2).

Example 7 :

√(x² – 3x)

Solution :

y  =  √(x² – 3x)

Here, radicand  x² – 3x is defined by non-negative numbers.

So set that expression,

x² – 3x ≥ 0

x(x – 3) ≥ 0

x  =  0 and x – 3  =  0

Now, we have to choose only positive.

So, the possible values of x are

x ≤ 0 or x ≥ 3

The domain is (-∞, 0] u [3, ∞)

Therefore, the required solution is x ≤ 0 or x ≥ 3

Example 8 :

√[(x+3)/(x-1)]

Solution :

y  =  √[(x+3)/(x-1)]

Here, radicand (x+3) and (x–1) in the numerator and denominator is defined by non-negative values of x and the denominator will not become 0.

Now, we have to choose only positive.

So, the possible values of x are

x ≤ -3 or x > 1

The domain is (-∞, -3] u (1, ∞)

Therefore, the required solution is x ≤ -3 or x > 1

Example 9 :

5/√(2x - 10)

Solution :

y  =  5/√(2x - 10)

y = 5/√2(x - 5)

Since at the denominator only we have radical function, to find the possible values which will not make the denominator as zero, we have to equate the denominator to 0.

√(2x - 10) = 0

2x - 10 = 0

2x = 10

x = 5

Domain is all real values except 5. R - {5}.

Example 10 :

√(x² - 36)/(2x - 8)

Solution :

y = √(x² - 36)/(2x - 8)

2x - 8 = 0

2x = 8

x = 4

√(x² - 36) ≥ 0

x² - 36 ≥ 0

x² ≥ 36

x² ≥ √36

x ≥ ±6

The intervals are 

(-∞, -6], [-6, 4) (4, 6] and [6, ∞)

• In the interval (-∞, -6], we get positive at numerator.
• In the interval [-6, 4), we get the negative at numerator.
• In the interval (4, 6], we get the negative at numerator.
• In the interval [6, ∞), we get the negative at numerator.

So, the required domain is (-∞, -6] U  [6, ∞)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.