HOW TO FIND DOT PRODUCT OF 2 VECTORS

Let a vector and b vector be any two non-zero vectors and θ be the included angle of the vectors. Their scalar product or dot product is denoted by a . b and is defined as a scalar |a vector||b vector| cos θ

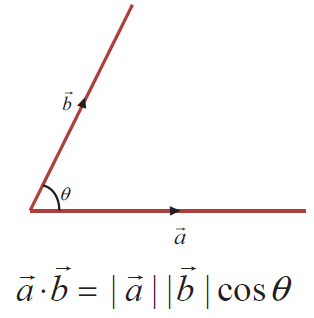
Working rule to find scalar product of two vectors

Let

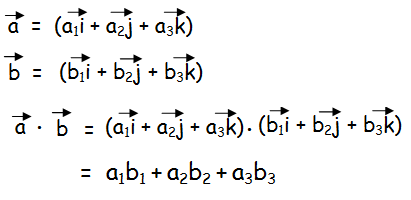
Hence, the scalar product of two vectors is equal to the sum of the products of their corresponding rectangular components.

Question  1 :

Find a vector . b vector when

(i) a vector = i vector−2 vector+k vector and

b = 3i vector  − 4j vector−2k vector

Solution :

a₁  =  1 , a₂  =  -2 and a₃  =  1

b₁  =  3 , b₂  =  -4 and b₃  =  -2

a . b  =  a₁b₁ + a₂b₂ + a₃b₃

a . b  =  1(3) + (-2)(-4) + 1(-2)

  =  3 + 8 - 2

  =  11 - 2

  =  9

Hence the dot product of above vectors is 9.

(ii) a = 2i vector + 2j vector − k vector and

b = 6i vector − 3j vector + 2k vector.

Solution :

a₁  =  2 , a₂  =  2 and a₃  =  -1

b₁  =  6 , b₂  =  -3 and b₃  =  2

a . b  =  a₁b₁ + a₂b₂ + a₃b₃

a . b  =  2(6) + 2(-3) + (-1)2

  =  12 - 6 - 2

  =  12 - 8

  =  4

Hence the dot product of above vectors is 4.

Find the missing components when two vectors are perpendicular

Question 2 :

Find the value λ are perpendicular, where

(i) a = 2i vector + λj vector + k vector and

b = i vector − 2j vector  + 3k vector

Solution :

If two vectors are perpendicular a vector . b vector  =  0

(2i  + λj + k) . (i - 2j + 3k)  =  0

2(1) + λ(-2) + 1(3)  =  0

2 - 2λ + 3  =  0

 5 - 2λ  =  0

2λ  =  5

λ  =  5/2

Hence the value of λ is 5/2.

(ii) a = 2i vector + 4j vector − k vector and

b = 3i vector − 2j vector +  λ k vector

Solution :

If two vectors are perpendicular a vector . b vector  =  0

(2i  + 4j - k) . (3i - 2j + λk)  =  0

2(3) + 4(-2) + (-1)(λ)  =  0

6 - 8 - λ  =  0

-2 - λ  =  0

λ  =  -2

Hence the value of λ is -2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.