HOW TO FIND EQUATION OF LOCUS OF A POINT WITH THE GIVEN DISTANCE

Example 1 :

Find the points on the locus of points that are 3 units from x-axis and 5 units from the point (5, 1).

Solution :

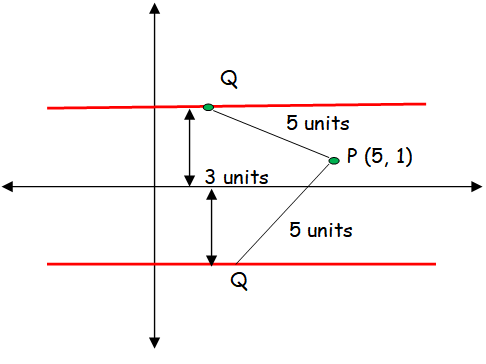
Let Q be (h, k)

• If the required point above the line, then it would be in the form (h, 3)
• If the required point above the line, then it would be in the form (h, -3)

PQ  =  5

P (5, 1) Q (h, 3)

PQ  =  √(x₂ - x₁)² + (y₂ - y₁)²

√(5 - h)² + (1 - 3)²  =  5

√((5 - h)² + 4)  =  5

Taking squares on both sides, we get

(5 - h)² + 4  =  25

(5 - h)²  =  25 - 4

(5 - h)²  =  21

(5 - h) =  √21

h  =  5 ± √21 

If the point is in above the line, then the required points would be  (5 + √21 , 3) or (5 - √21 , 3)

P (5, 1) Q (h, -3)

PQ  =  √(x₂ - x₁)² + (y₂ - y₁)²

√(5 - h)² + (1 + 3)²  =  5

√((5 - h)² + 16)  =  5

Taking squares on both sides, we get

(5 - h)² + 16  =  25

(5 - h)²  =  25 - 16

(5 - h)²  =  ±9

(5 - h) =  ± 3

h  =  5 - 3  (or)  h  = 5 + 3

h = 2 (or)  h = 8

If the point is in below the line, then the required point will be  (2 , -3) or (8, -3)

Example 2 :

The sum of the distance of a moving point from the points (4, 0) and (−4, 0) is always 10 units. Find the equation of the locus of the moving point

Solution :

Let P(h, k) be the moving point 

Let A (4, 0) and B (-4, 0)

PA + PB  =  10

√(h - 4)² + (k - 0)² + √(h + 4)² + (k - 0)²  =  10

√(h - 4)² + k²  =  10 - √(h + 4)² + k²

Taking squares on both sides,

(h - 4)² + k²  =  100 - 20√(h + 4)² + k² + (h + 4)² + k²

h²-8h+16+k²=100-20√((h + 4)²+k²)+h²+8h+16+k²

-16h - 100  =  -20√((h + 4)²+k²)

4h + 25  =  5√((h + 4)²+k²)

By taking squares on both sides, we get

16h² + 200h + 625  =  25 (h² + 8h + 16 + k²)

25h²-16h² + 25k² + 200h - 200h + 400 - 625  =  0

9h² + 25k² - 225  =  0

9h² + 25k² =  225

Divide by 225

h²/25 + k²/9  =  1

By replacing h and k by x and y respectively, we get

x²/25 + y²/9  =  1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.