HOW TO FIND EQUATION OF PARABOLA WITH VERTEX AND LATUS RECTUM

We can use the steps given below to find the equation of a parabola when its vertex and the equation of latus rectum are given.

Step 1 :

Sketch the graph of the parabola using the given vertex and equation of latus rectum.  

Once the graph of the parabola is sketched, you can know to which side the parabola opens. 

Step 2 :

Find the distance between vertex and focus to get the value of a.

Step 3 :

Using the results of steps 1 and 2, find the equation (Explained in the following examples). 

Example 1 :

Find the equation of the parabola whose vertex is (1, 2) and the equation of the latus rectum is x = 3.

Solution :

Sketch the parabola with vertex (1, 2) and equation of the latus rectum x = 3. 

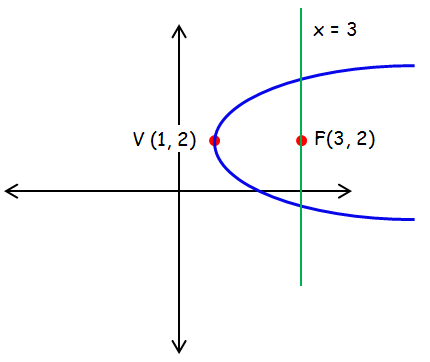
The parabola opens right.

Standard equation of the parabola that open right.

(y - k)²  =  4a(x - h)

Substitute vertex (h, k) = (1, 2).

(y - 2)²  =  4a(x - 1)

Distance between the vertex latus rectum, a = 2.

(y - 2)²  =  4(2)(x - 1)

(y - 2)²  =  8(x - 2)

Example 2 :

Find the equation of the parabola whose vertex is (1, 2) and the equation of the latus rectum is y = 5

Solution :

Sketch the parabola with vertex (1, 2) and equation of the latus rectum y = 5. 

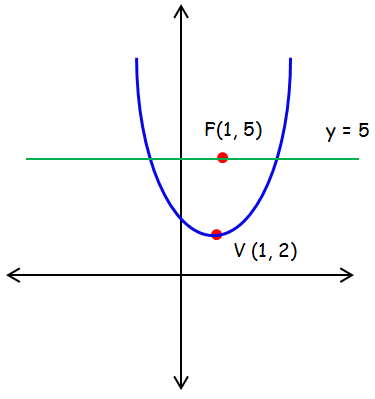
The parabola opens up.

Standard equation of the parabola that open up.

(x - h)²  =  4a(y - k)

Vertex (h, k) = (1, 2).

(x - 1)²  =  4a(y - 2)

Distance between the vertex latus rectum, a = 3.

(x - 1)²  =  4(3)(y - 2)

(x - 1)²  =  12(y - 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.