HOW TO FIND EXPANSION OF EXPONENTIAL FUNCTION

The series Σ(xⁿ/n!), where n ∈ [1, +∞) is called an exponential series. It can be proved that this series converges for all values of x.

For any real number x,

Σ(xⁿ/n!) where n ∈ [1, +∞)  =  e^x, where

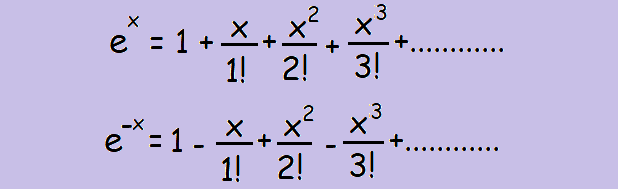
Some more results :

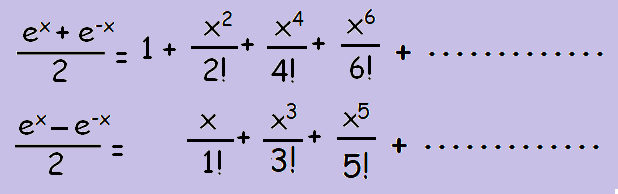
Solved Questions

Write the first 6 terms of each exponential series : 

Question 1 :

e^5x

Solution :

e^x  =  1 + (x/1!) + (x²/2!) + (x³/3!) + ..................

In the formula above, substitute x = 5x. 

e^5x :

=  1 + (5x/1!) + ((5x)²/2!) + ((5x)³/3!) + ((5x)⁴/4!) +  ((5x)⁵/5!) + ..................

=  1 + (5x/1!) + (25x²/2) + (125 x³/6) + (625 x⁴/24) +  (625 x⁵/24) + ..................

Question 2 :

e^-2x

Solution :

e^-x  =  1 - (x/1!) + (x²/2!) - (x³/3!) + ..................

In the formula above, substitute x = -2x.

e^-2x :

= 1 - (2x/1!) + ((2x)²/2!) - ((2x)³/3!) + ((2x)⁴/4!) - (2x)⁵/5!) + ..................

   =  1 - (2x/1!) + (4x²/2) + (8x³/6) + (16x⁴/24) +(32x⁵/120) + ..................

=  1 - 2x + 2x² + (4x³/3) + (2x⁴/3) + (4x⁵/15) + .........

Question 3 :

e^(1/2)x

Solution :

e^x  =  1 + (x/1!) + (x²/2!) + (x³/3!) + ..................

In the formula above, substitute x = x/2.

e^(1/2)x :

= 1 - (x/2/1!) + ((x/2)²/2!) - ((x/2)³/3!) + ((x/2)⁴/4!) -  ((x/2)⁵/5!) + ..................

=  1 - (x/2) + (x²/8) + (x³/48) + (x⁴/384) + (x⁵/3840) + .....

Logarithmic Expansion

The series Σ(−1)ⁿ⁺¹xⁿ /n, where n ∈ [1, +∞) is called a logarithmic series. This series converges for all values of x satisfying |x| < 1. This series converges when x = 1 also. For all values of x satisfying |x| < 1, the sum of the series is log(1 + x). Thus

log(1 + x)  =  x - (x²/2) + (x³/3) - (x⁴/4) + .......

for all values of x satisfying |x| < 1.

By taking -x in place of x, we get

log(1 - x)  =  -x - x²/2 - x³/3 - x⁴/4 .......

for all values of x satisfying |x| < 1.

Now, 

log [(1+x) / (1-x)]  =  log(1 + x) - log(1 - x)

Using this we get

log [ (1 + x)/(1 - x)]  = 2 [x + x³/3  + x⁵/5 +............]

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.