How to Find f o g and g o f From the Given Relation

Question 1 :

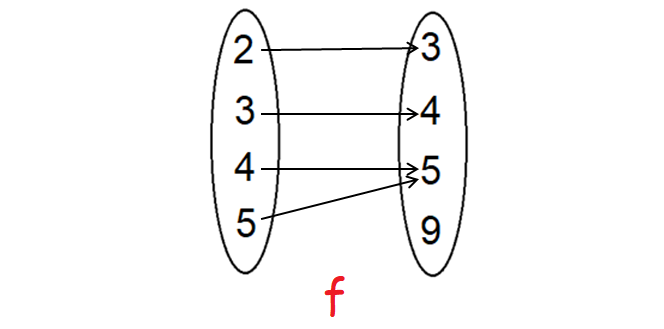
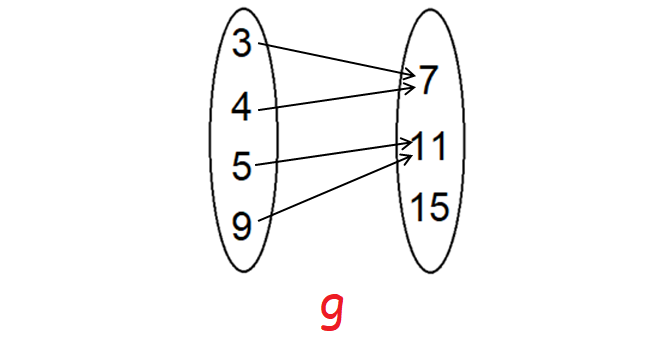
Let f : [2, 3, 4, 5] -> [3, 4, 5, 9] and g : [3, 4, 5, 9] -> [7, 11, 15] be functions defined as f(2) = 3, f(3) = 4, f(4) = f(5) = 5 and g(3) = g(4) = 7 and g(5) = g(9) = 11. Find g o f.

Answer :

Write the function f as a set of ordered pairs.

f = {(2, 3), (3, 4), (4, 5), (5, 5)}

Write the function g as a set of ordered pairs.

g = {(3, 7), (4, 7), (5, 11), (9, 11)}

g o f can be denoted as

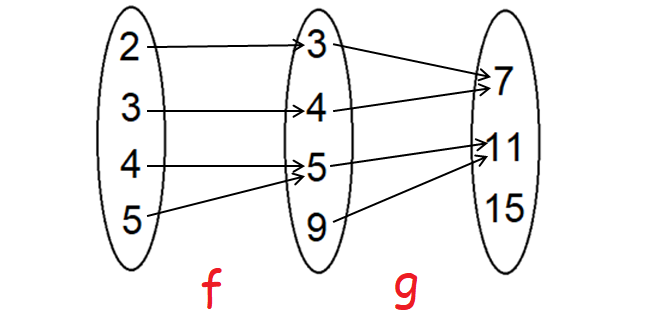
(g o f) (2) = 7

(g o f) (3) = 7

(g o f) (4) = 11

(g o f) (5) = 11

Therefore, g o f = {(2, 7), (3, 7), (4, 11), (5, 11)}.

Question 2 :

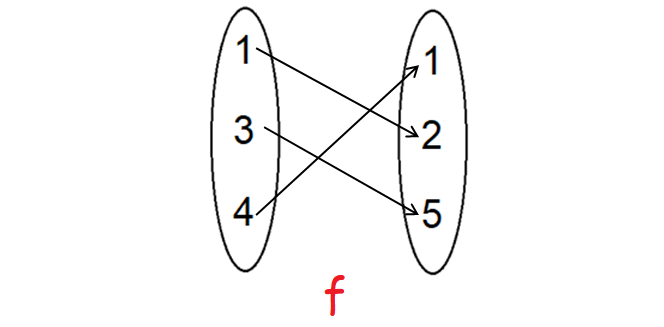
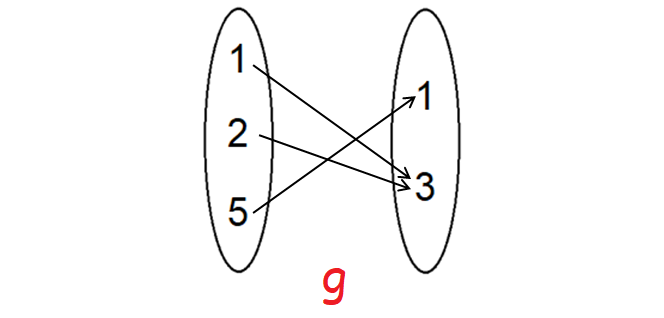
Let f : {1, 3, 4} -> {1, 2, 5} and g : {1, 2, 5} -> {1, 3} be given by f = {(1, 2) (3, 5) (4, 1)} and g = {(1, 3) (2, 3) (5, 1)}. Find g o f.

Answer :

f = {(1, 2) (3, 5) (4, 1)}

g = {(1, 3) (2, 3) (5, 1)}

g o f can be denoted as

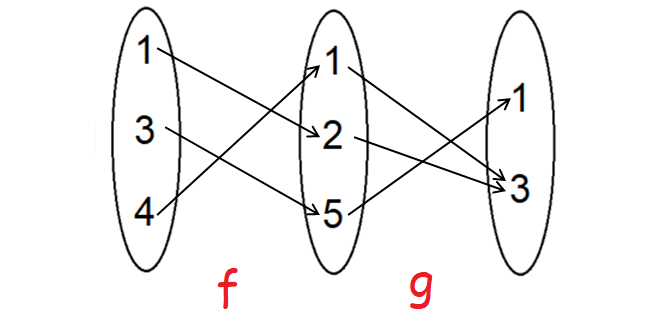
(g o f) (1) = 3

(g o f) (3) = 1

(g o f) (4) = 3

Therefore, g o f = {(1, 3), (3, 1), (4, 3)}.

Question 3 :

Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3), (4, 9), (5, 9)}. Show that g o f and f o g are defined. Also find f o g and g o f.

Answer :

f = {(3, 1), (9, 3), (12, 4)}

Domain  of f = {3, 9, 12} and Range of f = {1, 3, 4}

g = {(1, 3), (3, 3), (4, 9), (5, 9)}

Domain of g = {1, 3, 4, 5} and Range of g = {3, 9}

If f o g is defined, then range of g must be a subset of domain of f. {3, 9} is a subset of {3, 9, 12}.

So, f o g is defined.

If g o f is defined, then range of f must be a subset of domain of g = {1, 3, 4} is a subset of {1, 3, 4, 5}.

So, g o f is defined.

g o f :

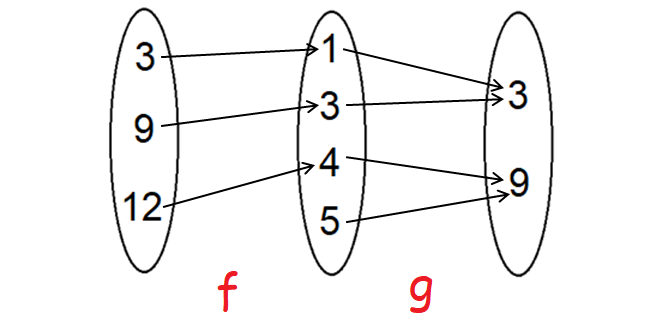
(g o f) (3) = 3

(g o f) (9) = 3

(g o f) (12) = 9

Therefore, g o f = {(3, 3), (9, 3), (12, 9)}.

f o g :

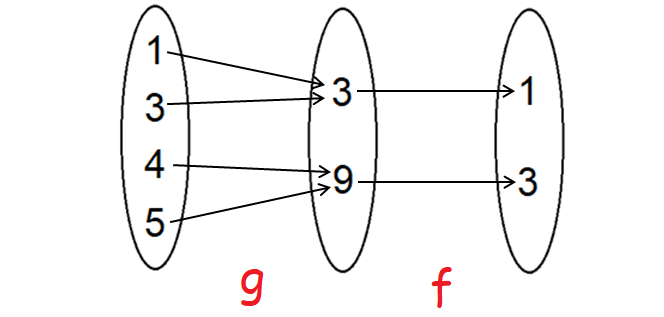
(f o g) (1) = 1

(f o g) (3) = 1

(f o g) (4) = 3

(f o g) (5) = 3

Therefore, f o g = {(1, 1), (3, 1), (4, 3), (5, 3)}.

Question 4 :

Let f = {1, -1), (4, -2), (9, -3), (16, 4)} and g = {(-1, -2), (-2, -4), (-3, -6), (4, 8)}. Show that g o f is defined while f o g is not defined. Also, find g o f.

Answer :

f = {1, -1), (4, -2), (9, -3), (16, 4)}

Domain of f = {1, 4, 9, 16} and Range of f = {-1, -2, -3, 4}

g = {(-1, -2), (-2, -4), (-3, -6), (4, 8)}.

Domain of g = {-1, -2, -3, 4} and Range of g = {-2, -4, -6, 8}

Since range of f is a subset of domain of g, g o f is defined.

Since range of g is not a subset of domain of f, f o g is not defined.

g o f :

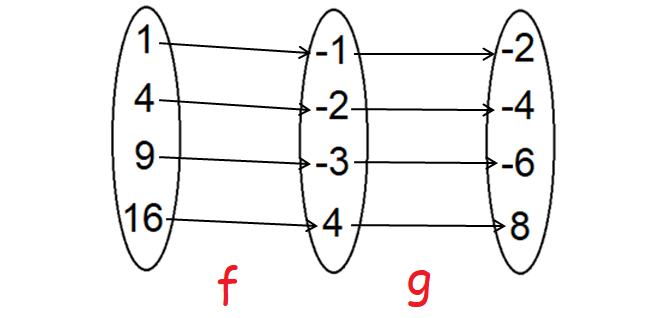
(g o f) (1) = -2

(g o f) (4) = -4

(g o f) (9) = -6

(g o f) (16) = 8

Therefore, f o g = {(1, -2), (4, -4), (9, -6), (16, 8)}.

Question 5 :

Find in the following table, given that h(x) = f(g(x))

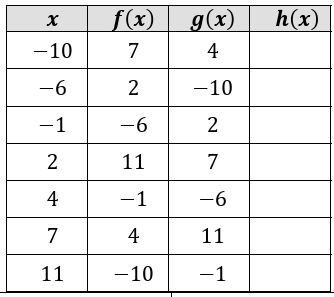
Solution :

Given that, h(x) = f(g(x))

When x = 11

h(11) = f(g(11))

= f(-1)

= -6

Question 6 :

Use the graph to find the following.

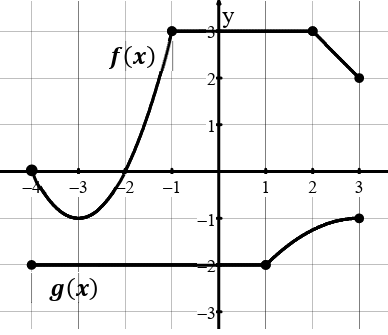
a)  Find f(g(1))

b) Find (f o g)(3)

c)  Find g(f(2))

Solution :

a)  f(g(1)) = f(-2)

f(g(1)) = 0

b) (f o g)(3) = f[g(3)]

= f(-1)

(f o g)(3) = 3

c)  g(f(2)) = g(3)

g(f(2)) = -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.