FIND THE DERIVATIVES FROM THE LEFT AND RIGHT AT THE GIVEN POINT

How to Find if the Function is Differentiable at the Point ? :

The function is differentiable from the left and right. As in the case of the existence of limits of a function at x₀, it follows that

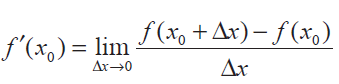
exists if and only if both

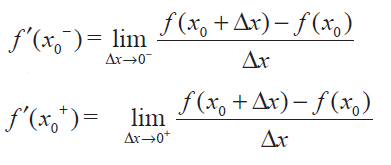
exist and f' (x₀-)  =   f' (x₀+) 

Hence 

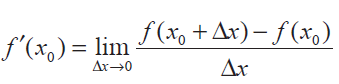
if and only if f' (x₀-)  =   f' (x₀+) . If any one of the condition fails then f'(x) is not differentiable at x_0.

Question 1 :

Determine whether the following function is differentiable at the indicated values.

(i) f(x) = x | x | at x = 0

Solution :

f(x) = x | x | 

If x < 0, then f(x) = x (-x)  =  -x² 

If x > 0, then f(x) = x (x)  =  x² 

f'(0^-)  =  lim _x->0- [(f(x) - f(0)) / (x - 0)]

  =  lim _x->0- (-x² - 0) / x

  =  lim _x->0- -x

  =  0  -----(1)

f'(0⁺)  =  lim _x->0+ [(f(x) - f(0)) / (x - 0)]

  =  lim _x->0+ (x² - 0) / x

  =  lim _x->0+ x

  =  0 -----(2)

f'(0^-)  =  f'(0⁺) 

Hence the given function is differentiable at the point x = 0.

(ii)  f(x) = |x² - 1| at x = 1

Solution :

f(x) = |x² - 1|

If x < 1, then f(x) = -(x² - 1) 

If x > 1, then  f(x) = (x² - 1) 

f'(1^-)  =  lim _x->1- [(f(x) - f(1)) / (x - 1)]

  =  lim _x->1- [(-x² + 1) - (0)] / (x - 1)

  =  lim _x->1- [-(x² - 1) / (x - 1)]

  =  lim _x->1- [-(x + 1)(x - 1) / (x - 1)]

=  -2  -----(1)

f'(1⁺)  =  lim _x->1+ [(f(x) - f(1)) / (x - 1)]

  =  lim _x->1+ [(x² - 1) - (0)] / (x - 1)

  =  lim _x->1+ [(x + 1)(x - 1) / (x - 1)]

  =  lim _x->1+ (x + 1)

=  2  -----(2)

f'(1^-)  ≠ f'(1⁺) 

Hence the given function is not differentiable at the point x = 1.

(iii)  f(x) = |x| + |x - 1| at x = 0, 1

Solution :

f(x) = |x| + |x - 1|

Check if the given function is continuous at x = 0.

If x < 0, then f(x) = -x - (x - 1)

f(x)  =  -x - x + 1

  =  -2x + 1

If x > 0 and x < 1, then f(x) = x - (x - 1)

f(x)  =  x - x + 1

  =  1

If x > 1, then f(x) = x + (x - 1)

f(x)  =  x + x + 1

  =  2x + 1

f'(0^-)  =  lim _x->0- [(f(x) - f(0)) / (x - 0)]

  =  lim _x->0- [(-2x + 1) - 1] / x

  =  lim _x->0- -2x / x

  =  lim _x->0- -2

  =  -2  -----(1)

f'(0⁺)  =  lim _x->0+ [(f(x) - f(0)) / (x - 0)]

  =  lim _x->0+ [1 - 1] / x

  =  lim _x->0- 0 / x

  =  0/0  -----(2)

f'(0^-)  ≠ f'(0⁺) 

f'(1^-)  =  lim _x->1- [(f(x) - f(1)) / (x - 1)]

  =  lim _x->1- [1 - 1] / (x - 1)

  =  lim _x->1- 0 / (x-1)

  =  0 -----(1)

f'(1⁺)  =  lim _x->1+ [(f(x) - f(1)) / (x - 1)]

  =  lim _x->1+ [2x + 1 - 3] / (x - 1)

  =  lim _x->1+ (2x - 2) / (x - 1)

  =  lim _x->1+ 2(x - 1) / (x - 1)

  =  2 -----(2)

f'(1^-)  ≠ f'(1⁺) 

Hence the given function is not differentiable at the given points.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.