HOW TO FIND IMAGE OF A POINT ABOUT THE LINE

Question 1 :

Find the image of the point (−2, 3) about the line x + 2y − 9 = 0.

Solution :

Let us draw a perpendicular line from the point (-2, 3). 

Now we have to find the equation of the line perpendicular to the line x + 2y - 9  =  0.

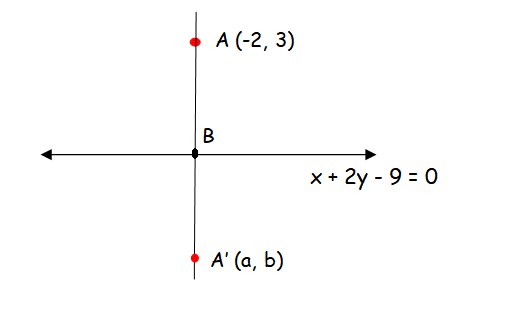
Let us find the line which is perpendicular to the line x + 2y - 9  =  0.

2x - y + k  =  0

The perpendicular line 2x - y + k  =  0 is passing through the point (-2, 3) 

2(-2) - 3 + k  =  0

-4 - 3 + k =  0

k  =  7

2x - y + 7  =  0

By solving the above two equations, we get the point B.

x + 2y - 9  =  0   -----(1)

2x - y + 7  =  0   -----(2)

Multiply the first equation by 2, we get

2x + 4y - 18  =  0

(1) - (2)

(2x + 4y - 18) - (2x - y + 7)  =  0

2x + 4y - 18 - 2x + y - 7  =  0

5y - 25  =  0

y  =  5

By applying the value of y in the first equation, we get

x + 2(5) - 9  =  0

x + 10 - 9  =  0

x + 1  =  0

 x  =  -1

B(-1, 5)

Mid point of AA'  =  (x₁ + x₂)/2, (y₁ + y₂)/2

(-2 + a) /2 , (3 + b)/2  =  (-1, 5)

Hence the required point is (0, 7)

Question 2 :

A line is drawn perpendicular to 5x = y + 7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 10 sq. units.

Solution :

5x - y - 7  =  0

The line which is perpendicular to the above line is 1x + 5y + k  =  0

By applying A(x, 0),  we get the value of x in terms of k.

1x + 5(0) + k  =  0

x + k  =  0

x  =  -k

By applying B(0, y),  we get the value of y in terms of k.

1(0) + 5y + k  =  0

5y + k  =  0

y  =  -k/5

here, x = base of triangle, y = height of triangle

Area of triangle  =  10 square units

(1/2) ⋅ Base ⋅ Height  =  10

(1/2) ⋅ (-k) ⋅ (-k/5)  =  10

k²  =  100  ==>  k  =  ± 10

 x + 5y  =  ± 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.