HOW TO FIND INVERSE OF A LOGARITHMIC FUNCTION
Before learning how to find inverse of a logarithmic function, you need to know how to convert an equation from logarithmic to exponential.
Consider the following equation in logarithmic form.
logam = x
The picture below illustrates how to convert the above equation from logarithmic to exponential form.
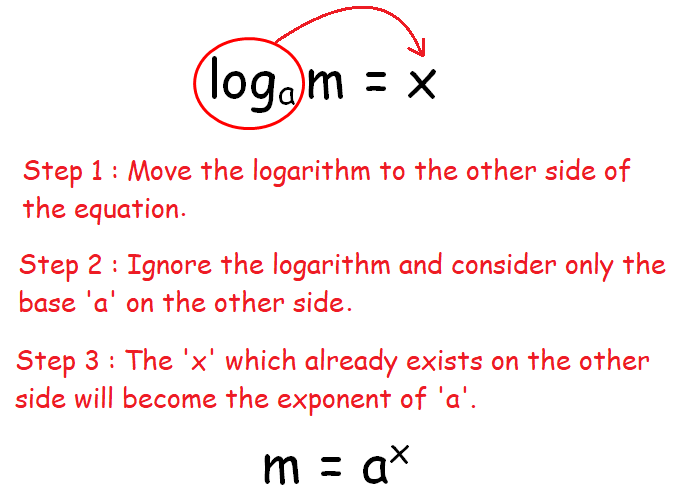
How to Find Inverse of a Function
The following steps would be useful to find inverse of a function f(x), that is f-1(x).
Step 1 :
Replace f(x) by y.
Step 2 :
Interchange the variables x and y.
Step 3 :
Solve for y.
Step 4 :
Replace y by f-1(x).
Example 1 :
Find f-1(x), if f(x) = log2(x).
Solution :
f(x) = log2(x)
Replace f(x) by y.
y = log2(x)
Interchange x and y.
x = log2(y)
The above equation is in logarithmic form. Convert it to exponential form.
2x = y
or
y = 2x
Replace y by f-1(x).
f-1(x) = 2x
Example 2 :
Find f-1(x), if f(x) = log5(5x + 2).
Solution :
f(x) = log5(5x + 2)
Replace f(x) by y.
y = log5(5x + 2)
Interchange x and y.
x = log5(5y + 2)
The above equation is in logarithmic form. Convert it to exponential form.
5x = 5y + 2
or
5y + 2 = 5x
Subtract 2 from both sides.
5y = 5x - 2
Divide both sides by 5.
y = (5x - 2)/5
Replace y by f-1(x).
f-1(x) = (5x - 2)/5
Example 3 :
Find g-1(x), if g(x) = -2ln(5 - 2x) + 8.
Solution :
g(x) = -2ln(5 - 2x) + 8
Replace g(x) by y.
y = -2ln(5 - 2x) + 8
Interchange x and y.
x = -2ln(5 - 2y) + 8
Subtract 8 from both sides.
x - 8 = -2ln(5 - 2y)
Divide both sides by -2.
(x - 8)/(-2) = ln(5 - 2y)
(8 - x)/2 = ln(5 - 2y)
In the equation above, we have natural logarithm 'ln' and its base is e. Convert it to exponential form.
e(8 - x)/2 = 5 - 2y
Add 2y to both sides.
e(8 - x)/2 + 2y = 5
Subtract e(8 - x)/2 from both sides.
2y = 5 - e(8 - x)/2
Divide both sides by 5.
y = (5 - e(8 - x)/2)/2
Replace y by g-1(x).
g-1(x) = (5 - e(8 - x)/2)/2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
