HOW TO FIND THE LENGTH OF LATUS RECTUM OF A PARABOLA

Consider the graph of a parabola shown below.

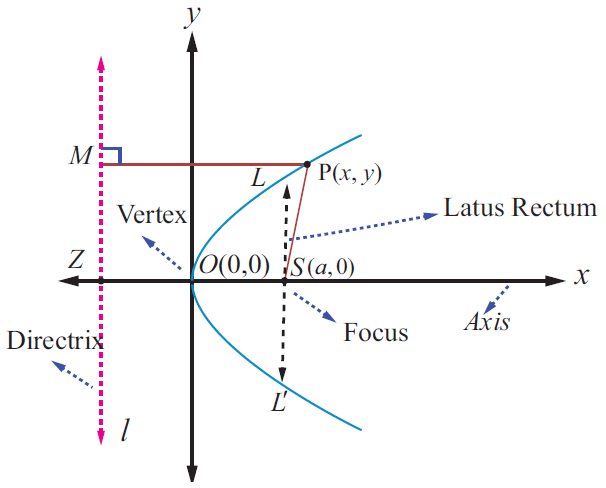
The parabola opens to the right with vertex (0, 0).

The equation of the parabola shown above in standard form :

y² = 4ax

Latus rectum LL' passes through the focus (a, 0).

Hence the point L is (a, y₁).

There fore,

y₁² = 4a(a)

y₁² = 4a²

Take square root on both sides.

y₁ = ±√(4a²)

y₁ = ±2a

y₁ = 2a or -2a

The end points of latus rectum are (a, 2a) and (a,-2a).

Therefore length of the latus rectum LL' = 4a.

Find the length of latus rectum of the following parabolas :

Example 1 :

x² = -4y

Solution :

The given equation equation of the parabola in standard form.

Comparing x² = -4y and x² = -4ay,

4a = 4

So, the length of latus rectum is 4 units.

Example 2 :

y² - 8x + 6y + 9 = 0

Solution :

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

y² - 8x + 6y + 9 = 0

y² + 6y = 8x - 93

y² + 2(y)(3) = 8x - 9

y² + 2(y)(3) + 3² - 3² = 8x - 9

(y + 3)² - 3² = 8x - 9

(y + 3)² - 9 = 8x - 9

(y + 3)² = 8x

(y + 3)² = 8(x - 0)

Now, the equation of the parabola is in standard form.

Comparing (y - k)² = 4a(x - h) and (y + 3)² = 8(x - 0),

4a = 8

So, the length of latus rectum is 8 units.

Example 3 :

x² - 2x + 16y + 17 = 0

Solution :

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

x² - 2x = -16y - 17

x² - 2(x)(1) = -16y - 17

x² - 2(x)(1) + 1² - 1² = -16y - 17

(x - 1)² - 1² = -16y - 17

(x - 1)² - 1 = -16y - 17

(x - 1)² = -16y - 16

(x - 1)² = -16(y + 1)

Now, the equation of the parabola is in standard form.

Comparing (x - h)² = -4a(y - k) and (x - 1)² = -16(y + 1),

4a = 16

So, the length of latus rectum is 16 units.

Example 4 :

y = 2x²+ 3x + 4

Solution :

The given equation of the parabola is not in standard form.

Write the equation of the parabola in standard form. 

y = 2x²+ 3x + 4

or

2x²+ 3x = y - 4

4a = 1/2 or 0.5

So, the length of latus rectum is 0.5 units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.