HOW TO FIND MISSING SIDES OF SIMILAR FIGURES

These figures are similar. Find x to 2 decimal places.

Example 1 :

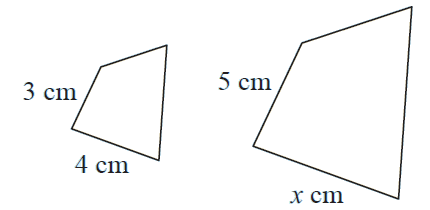
Solution :

Since the given shapes are similar, corresponding sides will be in the same ration.

3/4  =  5/x

3x  =  20

x  =  20/3

x  =  6.67 cm.

Example 2 :

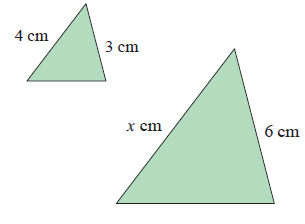
Solution :

Since the given figures are similar, the corresponding sides will be in the same ratio.

4/x  =  3/6

4(6)  =  3x

x  =  24/3

x  =  8 cm

Example 3 :

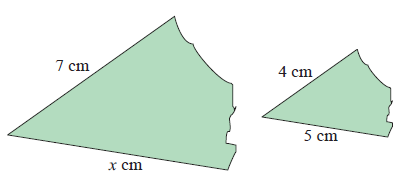
Solution :

Since the given figures are similar, the corresponding sides will be in the same ratio.

7/4  =  x/5

7(5)  =  4x

x  =  35/4

x  =  8.75 cm

Example 4 :

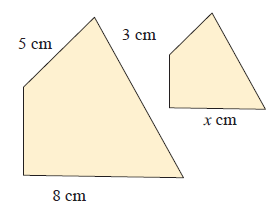
Solution :

Since the given figures are similar, the corresponding sides will be in the same ratio.

5/3  =  8/x

5x  =  8(3)

5x  =  24

x  =  24/5

x  =  4.8 cm

Example 5 :

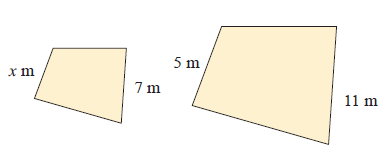
Solution :

Since the given figures are similar, the corresponding sides will be in the same ratio.

x/5  =  7/11

11x  =  7(5)

11x  =  35

x  =  35/11

x  =  3.18 cm.

Example 6 :

If a tree casts a 24-foot shadow at the same time that a yardstick casts a 2-foot shadow, find the height of the tree

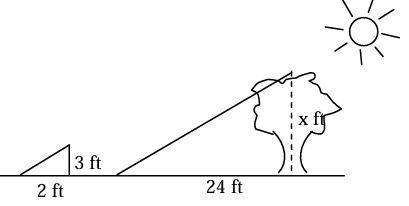
Solution :

Here x be the height of the tree. Since the triangles are similar, the corresponding sides will be in the same ratio.

2/3 = 24/x

Doing cross multiplication, we get

2x = 24(3)

x = 24(3)/2

= 12(3)

x = 36 ft

So, the height of the tree is 36 ft.

Example 7 :

A bush is sighted on the other side of a canyon. Find the width of the canyon.

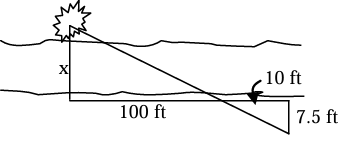
Solution :

Here x be the width of the canyon. Since the triangles are similar, the corresponding sides will be in the same ratio.

10/7.5 = 100/x

Doing cross multiplication, we get

10x = 100(7.5)

x = 100(7.5) / 10

x = 10(7.5)

= 75 ft

So, the width of the canyon is 75 ft.

Example 8 :

Sandy is trying to measure the height of a nearby flagpole using a mirror as shown in the diagram. The mirror is 6 meters away from the flagpole and 2 meters away from Sandy. The height of her eyes is 157 centimeters from which she can clearly see the top of the flagpole. How many centimeters tall is the flagpole ?

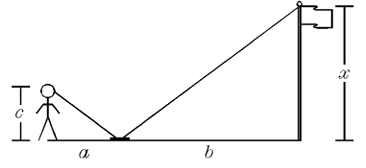
Solution :

From the information above and observing the picture, we get 

• The distance between mirror and flagpole (b) = 6 m
• b = 600 cm
• The distance between Sandy and mirror = 2 m
• a = 200 m
• Height of Sandy = 157 cm
• c = 157 cm

Since the triangles are similar, the ratio between corresponding sides will be equal.

x/b = c/a

x/600 = 157/200

x = 157(600)/200

x = 157(3)

= 471 cm

Height of the flagpole in centimeters is 471 cm.

Example 9 :

A 12-centimeter rod is held between a flashlight and a wall as shown. Find the length of the shadow on the wall if the rod is 45 cm from the wall and 15 cm from the light.

Solution :

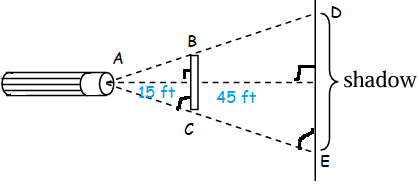
BC = 12 cm

In triangles ABC and ADE, 

<BAC = <DAE

<ACB = <AED

Using AA the triangles above are similar. By comparing the corresponding sides, we get

BC/DE = h₁/h₂

h₁ = 15 cm and h₂ = 15 + 45 ==> 60 cm

12/DE = 15/60

12/DE = 1/4

Doing cross multiplication, we get

4(12) = 1(DE)

DE = 48 cm

So, the length of the shadow is 48 cm.

Example 10 :

The cheerleaders at City High make their own megaphones by cutting off the small end of a cone made from heavy paper. If the small end of the megaphone is to have a radius of 2.5 cm, what should be the height of the cone that is cut off?

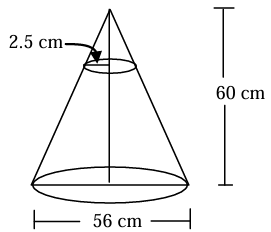
Solution :

Height of the small cone = h₁

Height of the large cone = h₂ ==> 60 cm

Radius of smaller cone = r₁ = 2.5 cm 

Radius of larger cone = r₂ = 56/2 ==> 28 cm

r₁/r₂ = h₁/h₂

2.5/28 = h₁/60

h₁ = 2.5(60)/28

= 150/28

h₁ = 5.35

So, the height of the cone cut off is 5.35 cm.

Example 11 :

Find the width of the Brady River.

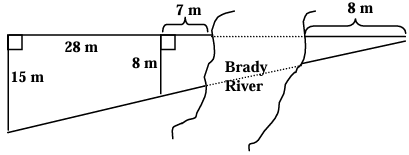
Solution :

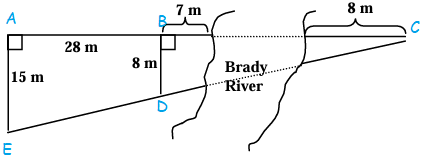
Let the width of the river be x.

BC = 7 + x + 8

= 15 + x

In triangles, ACE and BCD.

<CBD = <CAE

<BCD = <ACE

Using AA theorem triangles ACE and BCD are similar.

BD/AE = BC/CA

8/15 = (15 + x)/(15 + x + 28)

8/15 = (x + 15)/(43 + x)

8(43 + x) = 15(x + 15)

344 + 8x = 15x + 225

15x - 8x = 344 - 225

7x = 119

x = 119/7

x = 17

So, the width of the river is 17 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.