HOW TO FIND PATTERN MODEL FROM GIVEN TABLE

For the following input numbers and output numbers, find the rule in the number crunching machine :

Example 1 :

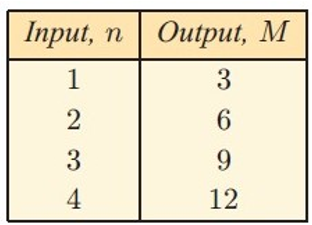
Solution :

By observing the output values each values is consecutive multiples of 3.

Let x and y be input and output values respectively.

By following rule, we get

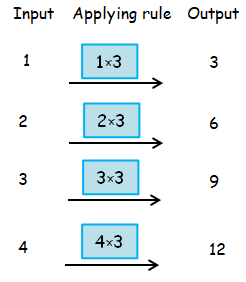
So, the required rule is M  =  3n

Example 2 :

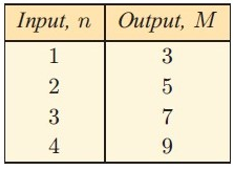
Solution :

Let x and y be the input and output values respectively.

By observing the output values each values is consecutive odd integers starts with 3.

Multiple of 2 nearest to 3 are 2 and 4.

2x is the even number, to get 3 we add 1 with 2x.

4x is also even number, to get 3 we should subtract 1 from 4x. So, the general term may be 4x-1.

Since it is not working when the inputs are 2, 3 and so on. So, we choose 2x+1.

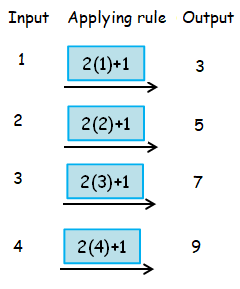
So, the required rule is M  =  2n+1

Example 3  :

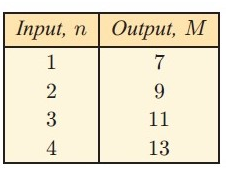
Solution :

By observing the output values each values is odd numbers, but it starts with 7.

By following rule, we get

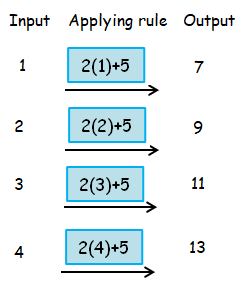
So, the required rule is M  =  2n+5.

Example 4  :

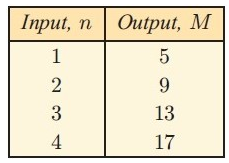
Solution :

The outputs are not consecutive. The even number nearest to 5 is 4.  To create a multiple of 4, we use 4x+1.

By following rule, we get

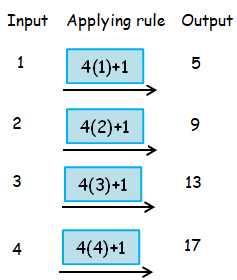
So, the required rule is M  =  4n+1.

Example 5 :

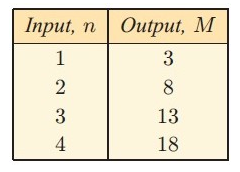
Solution :

Difference of each consecutive terms is 5. So, let us fix multiple of 5.

To get multiple of 5, we use 5x.

First term is multiple of 5 but it is less than 2.So, the general term is 5x-2.

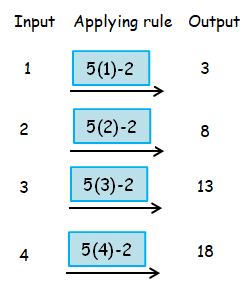
So, the required rule is M  =  5n-2.

Example 6 :

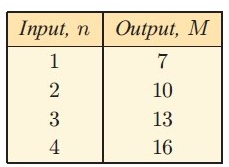
The difference of each consecutive terms is 3.

So, let us use 3x to get multiples of 3. To get 7 we should use 3x+4.

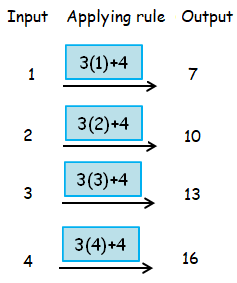
So, the required formula is M  =  3n+4.

Example 7 :

Start at 32 and divide by 2 each time. The fourth term is 

Solution :

• First term = 32
• Second term = 32/2 ==> 16
• Third term = 16/2 ==> 8
• Fourth term = 8/2 ==> 4

So, the required fourth term is 4.

Example 8 :

Start at 50 and subtract 4 each time. The eighth term is 

Solution :

• First term = 50
• Second term = 50 - 4 ==> 46
• Third term = 46 - 4 ==> 42
• Fourth term = 42 - 4 ==> 38

So, the required fourth term is 38.

Example 9 :

Start at 2 and multiply by 4 each time. The third term is

Solution :

• First term = 2
• Second term = 2 x 4 ==> 8
• Third term = 8 x 4 ==> 32
• Fourth term = 32 x 4 ==> 128

So, the required fourth term is 38.

Example 10 :

A plant that is 17 cm tall grows 2 cm each week.

a) Continue the sequence. 17, ___, ____, ___

b) How tall will the plant be after three weeks?

c) After how many weeks will the plant be 27 cm tall?

Solution :

Initial height = 17 cm

• Height of tree in the 1st week = 17 + 2 ==> 19 cm
• Height of tree in the 2nd week = 19 + 2 ==> 21 cm
• Height of tree in the 3rd week = 17 + 2 ==> 19 cm

b) after three weeks the height of the tree is 19 cm.

Creating a rule,

Height = 17 + 2n

Here n represents the number of weeks.

c) Applying height = 27, we get

27 = 17 + 2n

27 - 17 = 2n

2n = 10

n = 5

So, after 5 weeks the height of the tree will be 27 cm.

Example 11 :

Make a pattern to solve the problem.

a) Hanna has $49. She spends $8 each day.

How much money does she have left after 5 days?

Solution :

Amount she has initially = 48

Amount spent on each day = 8

Creating rule, we get

= 48 - 8n

Here n represents the number of days.

Amount she will have after 5 days :

= 48 - 8(5)

= 48 - 40

= 8

So, $8 is the amount leftover after 5 days.

Example 12 :

Six people start a new town. Every 20 years, the population doubles. After how many years will the town have more than 100 people?

Solution :

Initial population = 6

Every 20 years, the population will become double.

• After 20 years = 6(2) ==> 12
• After 40 years = 12 (2) ==> 24
• After 60 years = 24 (2) ==> 48
• After 80 years = 48 (2) ==> 96
• After 100 years = 96 (2) ==> 192

After 80 years the population will be move than 100.

Example 13 :

Ava has $30. She makes $8 an hour cutting lawns. She wants to buy a sweater that costs $86. How many hours does she have to work?

Solution :

Amount Ava has = 30

Charge per hour = $8

Cost of sweater = $86

30 + 8n = 86

Let n be the number of hours she is working.

8n = 86 - 30

8n = 56

n = 56/8

n = 7

She needs to work 7 hours.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.