HOW TO FIND RADIUS OF CIRCLE WHEN LENGTH OF CHORD IS GIVEN

Here we are going to see how to find radius of circle when length of chord is given.

To find the length of chord, we may use the following theorem

• Perpendicular from the centre of a circle to a chord bisects the chord.

Example 1 :

A chord of length 20 cm is drawn at a distance of 24 cm from the centre of a circle. Find the radius of the circle.

Solution :

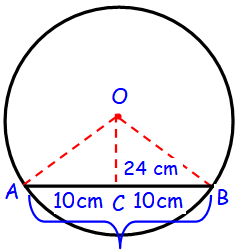
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

OB²  =  24² + 10²

BC²  =  576 + 100

BC²  =  676

BC  =  √676

BC  =  √(26 ⋅ 26)

BC  =  26  cm

Hence the radius of the circle is 26 cm.

How to find distance of chord from center ?

Example 2 :

A chord of length 16 cm is drawn in a circle of radius 10 cm. Find the distance of the chord from the centre of the circle.

Solution :

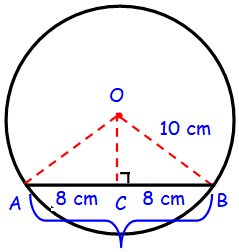
AB is a chord of length 16 cm

C is the midpoint of AB.

OB is the radius of length 10 cm

AB = 16 cm

AC = (1/2) ⋅ 16 = 8 cm

OB = 10 cm

In a right triangle OAC.

OC² = OA² - AC²

  =   √(10² - 8²)

  =   √(100 - 64)

  =   √36 cm

OC  =  6 cm

Hence, the distance of the chord from the centre is 6 cm

Example 3 :

The radius of a circle is 15 cm and the length of one of its chord is 18 cm. Find the distance of the chord from the centre.

Solution :

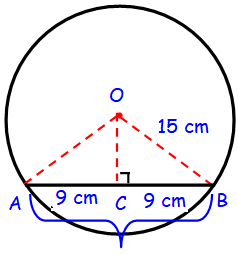
AB is a chord of length 18 cm

C is the midpoint of AB.

OB is the radius of length 10 cm

AB  =  18 cm

AC  =  (1/2) ⋅ 18  =  9 cm

OB = 15 cm

In a right triangle OCB.

OC² = OB² - BC²

  =   √(15² - 9²)

  =   √(225 - 81)

  =   √144

OC  =  12 cm

Hence the distance of chord from the center is 12 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.