HOW TO FIND RATIONAL NUMBERS BETWEEN TWO NUMBERS

Question 1 :

Which arrow best shows the position of 11/3 on the number line?

Solution :

Decimal form 11/3 is 3.666......

The arrow D represents this position.

Question 2 :

Find any three rational numbers between -7/11 and 2/11

Solution :

The given fractions are having same denominator. Rational numbers between the given fractions are

-6/11, -5/11, -4/11, -3/11, -2/11, -1/11, 0/11, 1/11

Question 3 :

Find any five rational numbers between

(i)  1/4 and 1/5

Solution :

a = 1/4, b = 1/5

To find the 1st rational number a and b, we have to find average of a and b.

c  =  (a + b)/2

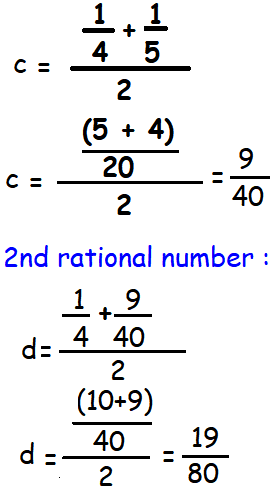
3rd rational number :

  =  [(1/4) + (19/80)]/2

  =  (20 + 19)/160

  =  39/160

4th rational number :

  =  [(1/4) + (39/160)]/2

  =  (40 + 39)/320

  =  79/320

5th rational number :

  =  [(1/4) + (79/320)]/2

  =  (80 + 119)/640

  =  159/640

Hence the 5 rational numbers are 

9/40, 19/80, 39/160, 79/320, 159/640.

(ii)  0.1 and 0.11

Solution :

Decimals lie between 0.1 and 0.11 are

0.101, 0.102, 0.103, 0.104, 0.105, 0.106, ............

(iii)  -1 and -2

Solution :

let a, b, c, d, e be the rational numbers between -1 and -2

a  =  [-1 + (-2)] /2  =  -3/2

b  =  [-1 + (-3/2)]/2  =  -5/4

c  =  [-1 + (-5/4)]/2  =  -9/8

d  =  [-1 + (-9/8)]/2  =  -17/16

e  =  [-1 + (-17/16)]/2  =  -33/32

Hence 5 rational numbers between -1 and -2 are -3/2, -5/4, -9/8, -17/16 and -33/32.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.