HOW TO FIND THE AREA OF A RHOMBUS WITH VERTICES

Let d₁ and d₂ be the lengths of the diagonals of a rhombus.

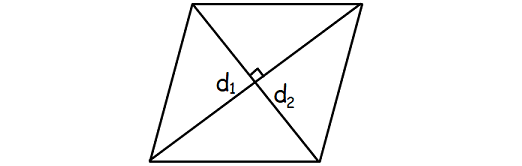
Formula for area of a rhombus :

If the four vertices of a rhombus are given, find the length of each diagonal using distance formula and find the area of the rhombus using the formula given above.

Distance between the two points (x₁, y₁) and (x₂, y₂) :

Example 1 :

Find the area of a rhombus with the following vertices taken in order.

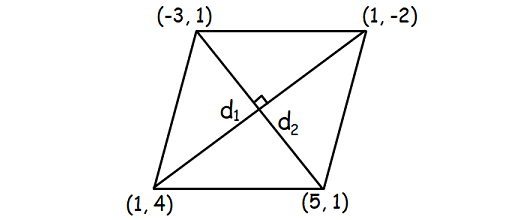
(1, 4), (5, 1), (1, -2), (-3, 1)

Solution :

Length of of diagonal d₁ :

d₁ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (1, 4) and (x₂, y₂) = (1, -2).

d₁ = √[(1 - 1)² + (-2 - 4)²]

= √[0 + (-6)²]

= √36

= 6

Length of of diagonal d₂ :

d₂ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (5, 1) and (x₂, y₂) = (-3, 1).

d₂ = √[(-3 - 5)² + (1 - 1)²]

= √[(-8)² + 0]

= √64

= 8

Area of rhombus :

= (1/2) x d₁ x d₂

Substitute d₁ = 8 and d₂ = 6.

= (1/2) x 8 x 6

= 24 square units

Example 2 :

Find the area of a rhombus with the following vertices taken in order.

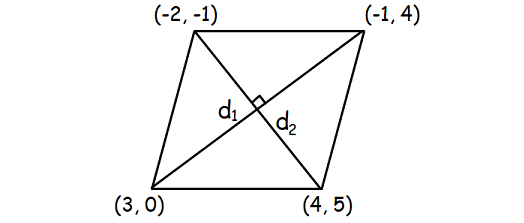
(3, 0), (4, 5), (-1, 4), (-2, -1)

Solution :

Length of of diagonal d₁ :

d₁ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (3, 0) and (x₂, y₂) = (-1, 4).

d₁ = √[(-1 - 3)² + (4 - 0)²]

= √[(-4)² + 4²]

= √[16 + 16]

= √32

= √(2 x 16)

= 4√2

Length of of diagonal d₂ :

d₂ = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (4, 5) and (x₂, y₂) = (-2, -1).

d₂ = √[(-2 - 4)² + (-1 - 5)²]

= √[(-6)² + (-6)²]

= √[36 + 36]

= √72

= √(2 x 36)

= 6√2

Area of rhombus :

= (1/2) x d₁ x d₂

Substitute d₁ = 4√2 and d₂ = 6√2.

= (1/2) x 4√2 x 6√2

= 24 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.