HOW TO FIND THE AREA OF THE SECTOR

Area of a sector is the region bounded by the bounding radii and the arc of the sector.

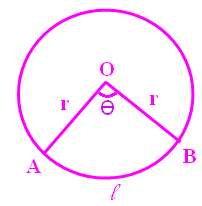
There are two methods to find the area of a sector.

(i) when the central angle and the radius are given

(ii) when length of arc and the radius are given

Area of a sector : 

=  (θ/360) ⋅ πr² square units

(or)

=  (lr/2) square units  

θ - central angle formed by the sector

L - length of arc

r - radius of the sector

We can use the first formula if the central angle(θ) formed by the sector and radius are given. If the length of arc(L) are given,  we have to use the second formula.

Area of Sector When Angle and Radius are Given  

Example 1 :

Find the area of the sector whose radius and central angle are 42 cm and 60° respectively.

Solution :

Area of the sector :

=  (θ/360°) ⋅ πr²

Substitute r = 42 cm , θ = 60°. 

=  (60°/360°) ⋅ π ⋅ 42²

=  (60°/360°) ⋅ π ⋅ 42 ⋅ 42

=  (1/6) ⋅ π ⋅ 42 ⋅ 42

=  294π cm²

Example 2 :

Find the area of the sector whose radius and central angle are 21 cm and 60° respectively.

Solution:

Area of the sector :

=  (θ/360°) ⋅ πr²

Substitute r = 21 cm , θ = 60°. 

=  (60°/360°) ⋅ π ⋅ 21²

=  (1/6) ⋅ π ⋅ 21 ⋅ 21

=  73.5π cm²

Example 3 :

Find the area of the sector whose radius and central angle are 4.9 cm and 30° respectively.

Solution :

Area of the sector : 

=  (θ/360°) ⋅ πr²

Substitute r = 4.9 cm , θ = 30°. 

=  (30°/360°) ⋅ π ⋅ 4.9²

=  (1/12) ⋅ π ⋅ 4.9 ⋅ 4.9

≈  73.5π cm²

Area of Sector When Length of Arc and Radius are Given

Example 4 :

Find the area of the sector and also find the central angle formed by the sector whose radius is 21 cm and length of arc is 66 cm (Use π ≈ 22/7).

Solution :

Area of the sector : 

=  (lr/2) square units

Substitute l = 66 and r = 21.

= (66 ⋅ 21)/2

=  693 cm²

Central angle formed by the sector : 

Area of sector  =  693 cm²

(θ/360)⋅ πr²  =  693

Substitute the known values and solve for θ. 

(θ/360)⋅ (22/7)(21)²  =  693

1386θ/360  =  693

77θ/20  =  693

Multiply each side by 20/77.

θ = 180°

Example 5 :

Find the area of the sector whose radius and length of arc are 6 cm and 20 cm.

Solution :

Area of the sector : 

=  (lr/2) square units

Substitute l = 6 and r = 20.

= (6 ⋅ 20)/2

=  60 cm²

Example 6 :

Find the area of the sector whose diameter and length of arc are 10 cm and 40 cm respectively.

Solution :

Radius  =  Diameter /2

=  10/2

=  5 cm

Area of the sector : 

=  (lr/2) square units

Substitute l = 40 and r = 5.

= (40 ⋅ 5)/2

=  100 cm²

How to Find the Area From the Given Perimeter 

Example 7 :

Find the area of the sector whose radius is 35 cm and perimeter is 147 cm.

Solution :

Perimeter of sector  =  147 cm

l + 2r  =  147

l + 2(35)  =  147

l + 70  =  147

l  =  77 cm

Area of the sector :

=  (lr)/2 square units

Substitute l = 77 and r = 35.

= (77 ⋅ 35)/2

=  1347.5 cm²

Example 8 :

Find the area of the sector whose radius is 20 cm and perimeter is 110 cm.

Solution :

Perimeter of sector  =  110 cm

l + 2r  =  110

l + 2(20)  =  110

l + 40  =  110

l  =  70 cm

Area of the sector :

=  (lr)/2 square units

Substitute l = 70 and r = 20.

= (70 ⋅ 20)/2

=  700 cm²

Example 8 :

In a xy plane below, O is the center of circle and the measure of <AOD is π/3. If the radius of circle O is 6, what is the length of AD ?

a)  3      b)  3√2      c)  4.5     d)  3√3

Solution :

<AOD = π/3

Radius of the circle = OA

sin θ = Opposite side / Hypotenuse

sin π/3 = AD / OA

√3/2  = AD / 6

AD = (√3/2) x 6

AD = 3√3

Example 9 :

In the xy-plane above, O is the center of the circle, and the measure of <POQ is kπ radians. What is the value of k ?

Solution :

<POQ = kπ

tan θ = Opposite side / Adjacent side

tan kπ = 1/1

tan kπ = 1

kπ = tan^-1(1)

kπ = π/4

So, the value of k is 1/4.

Example 10 :

In the -xy plane above, O is the center of the circle, and the measure of ∠POQ is a degree.

Solution :

tan θ = Opposite side / Adjacent side

tan (180 - a) = -√3/1

(180 - a) = tan^-1(-√3)

(180 - a) = 120

a = 180 - 120

a = 60

So, the value of a is 60 degree.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.