HOW TO FIND THE DETERMINANT OF A 3X3 MATRIX

Let A is 3x3 matrix,

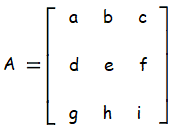
Here,

Number of rows of the required matrix is 3.

Number of columns of the required matrix is 3.

The determinant of the matrix A is calculated as,

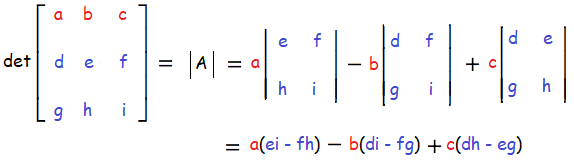
Note :

• If |A| = 0, then it is a singular matrix.
• If |A| ≠ 0, then it is a non singular matrix.

Example 1 :

Solution :

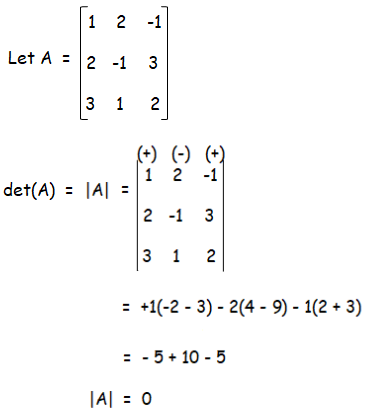
So, the determinant of A is 0

Example 2 :

Solution :

|A| =  +2(0 - 4) - 3(-1 + 0) - 1(-1 + 0)

=  -8 + 3 + 1

=  -8 + 4

|A| =  -4

So, the determinant of A is -4

Example 3 :

Solution :

|B| =  + 0(0 - 1) - 1(0 - 2) + 2(1 - 0)

=  2 + 2

=  4

So, the determinant of B is 4

Example 4 :

Solution :

|A| = +2(0 - 6) - 1(1 - 2) + 1(-3 + 0)

=  -12 + 1 - 3

=  -14

So, the determinant of A is -14

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.