HOW TO FIND THE EQUATION OF A LINE WITH ONE POINT

Question 1 :

Write the equations of the straight lines parallel to x-axis which are at a distance of 5 units from the x-axis

Solution :

The line which is drawn from above the x axis and parallel to the x axis will be a horizontal line.

So, the required equations will be y = 5 and y = -5.

Question 2 :

Find the equations of the straight lines parallel to the coordinates axes and passing through the point (-5, -2)

Solution :

via one point, we can draw infinite number of lines. Since the required lines will be parallel to x and y axis, we can draw two lines as follows.

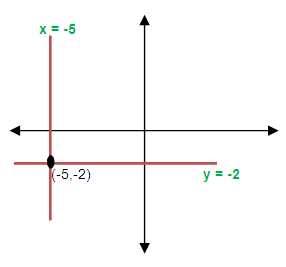
Therefore the two required equations are

y = -2 and x = -5.

Question 3 :

Find the equation of a straight line whose

(i) Slope is -3 and y-intercept is 4.

Solution :

Slope (m)  =  -3

Y-intercept (b)  =  4

Equation of the straight line:

y  =  mx + b

y  =  3x + 4

So, the required equation of the line y = 3x+4.

(ii) Angle of inclination is 60 degree and y-intercept is 3.

Solution :

Slope (m)  =  tan  θ

m  =  tan 60

m  =  √3

y-intercept (b) = 3

Equation of the straight line :

y  =  mx + b

y  =  √3x + 3

So, the required equation of the line y = √3x + 3.

Question 4 :

Find the equation of the line intersecting the y-axis at a distance of 3 units above the origin and

tan  θ = 1/2

where Ѳ is the angle of inclination.

Solution :

The required line is intersecting the y-axis at a distance of 3 units above the origin. So we can take y-intercept as 3

tan θ  =  1/2

m  =  1/2

Equation of the straight line :

y  =  mx + b

y  =  (1/2)x + 3

y  =  (x + 6)/2

2y  =  x + 6

x – 2y + 6  =  0

Question 5 :

Find the equation of the straight line which passes through the midpoint of the line segment joining

(4, 2) and (3, 1)

whose angle of inclination is 30 degree.

Solution :

First we have to find midpoint of the line segment joining the points (4, 2) and (3, 1)

Midpoint  =  (x₁ + x₂)/2, (y₁ + y₂)/2

=  (4 + 3)/2, (2 + 1)/2

=  (7/2, 3/2)

angle of inclination  =  30°

θ  =  30°

Slope (m)  =  tan θ

m  = tan 30°

m  =  1/√3

Equation of the line :

(y - y₁)  =  m(x - x₁)

(y - (3/2))  =  (1/√3)(x - (7/2))

(2y - 3)  =  (1/√3)(2x - 7)

2√3y - 3√3  =  2x - 7

2x - 2√3y - 7 + 3√3 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.