HOW TO FIND THE LENGTH OF A MEDIAN OF A TRIANGLE WITH VERTICES

Example 1 :

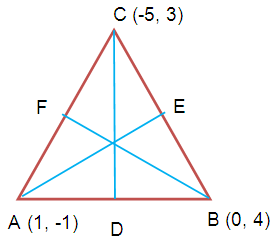
Find the length of the medians of the triangle whose vertices are (1 , -1) (0, 4) and (-5, 3)

Solution :

Let A (1, -1) B (0, 4) and C (-5, 3) are the points vertices of the triangle

Let D, E and F are the midpoints of the sides AB, BC and CA respectively 

Midpoint of AB = (x₁+x₂)/2 , (y₁+y₂)/2

=  (1+0)/2 , (-1+4)/2

=  D  (1/2, 3/2)

Midpoint of BC = (x₁+x₂)/2 , (y₁+y₂)/2

  =  (0+(-5))/2 , (4+3)/2

  =  (0-5/2 , 7/2)

  =  E  (-5/2, 7/2)

Midpoint of CA = (x₁+x₂)/2 , (y₁+y₂)/2

  =  (-5+1)/2 , (3+(-1))/2

  =  (-4/2 , 2/2)

  =  F  (-2, 1)

Length of the median AD = √(x₂-x₁)² + (y₂-y₁)²

A (1, -1)  and D  (1/2,3/2)

=  √(1+5/2)² + (-1-7/2)²

=  √(7/2)² + (-9/2)²

=  √(49/4)+(81/4)

=  √(49+81)/4

=  √130/4

=  √130/2

Length of the median BE = √(x₂-x₁)² + (y₂-y₁)²

B (0, 4) and E  (-5/2, 7/2)

  =  √(-2-0)² + (1-4)²

  =  √(-2)² + (-3)²

  =  √4+9

  =  √13

Length of the median CF = √(x₂-x₁)² + (y₂-y₁)²

C (-5, 3) and  F  (-2, 1)

  =  √((1/2)+5)² + ((3/2)-3)²

  =  √(11/2)² + (-3/2)²

  =  √(121/4)+(9/4)

  =  √(121 + 9)/4

  =  √130/4

  =  √130/2

Hence length of medians AD, BE and CF are  √130/2,  √13 and √130/2.

Example 2 :

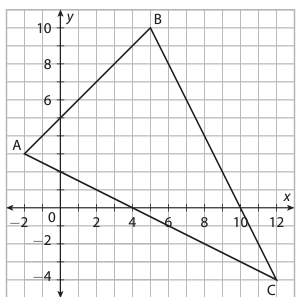
The vertices of a triangle are A (-2, 3), B (5, 10), and C (12, -4). Find the coordinates or equations for each feature of the triangle.

a) the coordinates of the midpoint of AC

b) the coordinates of the midpoint of BC

c) the equation of the line that contains the median through point B

d)  the equation of the line that contains the median through point A

e) the coordinates of the intersection of the two medians

f) the coordinates of the center of balance of the triangle

Solution :

A (-2, 3), B (5, 10), and C (12, -4).

a) Midpoint of AC = (x₁ + x₂)/2, (y₁ + y₂)/2

= (-2 + 12)/2, (3 - 4)/2

= 10/2, -1/2

= (5, -1/2)

Midpoint of AC = (5, -1/2)

b) Midpoint of BC = (5 + 12)/2, (10 - 4)/2

= 17/2, 6/2

= (17/2, 3)

c)  By drawing the median through B, it will pass through the midpoint of AC.

Equation of median :

y - y₁ = m(x - x₁)

B (5, 10) and (5, -1/2)

slope = (y₂ -y₁) / (x₂ - x₁)

= (-1/2 - 10) / (5 - 5)

 = (-21/2)/0

= undefined

the equation of the line that contains the median through point B

y - 10 = 1/0(x - 5)

0 = x - 5

x - 5 = 0 is the equation of median passes through the vertex B.

d)  the equation of the line that contains the median through point A

Equation of median :

y - y₁ = m(x - x₁)

A (-2, 3) and  (17/2, 3)

slope = (y₂ -y₁) / (x₂ - x₁)

= (3 - 3) / (17/2 + 2)

= 0

y - 3 = 0(x + 2)

y - 3 = 0

So, y - 3 = 0 is the required equation 

e) The point of intersection of these two medians is at (5, 3).

f) Centroid will be the point of intersections of all medians.

A (-2, 3), B (5, 10)

= (-2 + 5)/2, (3 + 10)/2

= (3/2, 13/2)

Finding centroid :

(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

(5, -1/2) (17/2, 3) and (3/2, 13/2)

= (5 + 17/2 + 3/2) / 3, (-1/2 + 3 + 13/2)/3

= (10 + 17 + 3)/6, (-1 + 6 + 13)/6

= 30/6, 18/6

= (5, 3)

Centroid of the triangle is (5, 3).

Example 3 :

∆𝐴𝐵𝐶 has vertices 𝐴(3,4), 𝐵(−5,2), and 𝐶(1,−4). Determine an equation for

a) the median from C to AB

b) the altitude from A to BC

c) the right bisector of AC

Solution :

Midpoint of AB :

A(3, 4) and 𝐵(−5,2)

= (3 - 5)/2, (4 + 2)/2

= -2/2, 6/2

= (-1, 3)

a) equation of median from C to AB :

𝐶(1,−4) and (-1, 3)

y - y₁ = m(x - x₁)

slope = (y₂ -y₁) / (x₂ - x₁)

= (3 + 4)/(-1 - 1)

= 7/-2

= -7/2

y - (-4) = (-7/2)(x - 1)

y + 4 = (-7/2) (x - 1)

2(y + 4) = -7(x - 1)

2y + 8 = -7x + 7

7x + 2y = 7 - 8

7x + 2y = -1

b) the altitude from A to BC

Slope of altitude of BC = -1/slope of BC

𝐵(−5,2), and 𝐶(1,−4)

= - 1/[(-4 - 2) / (1 + 5)]

= -1/-1

= 1

Equation of altitude from A :

𝐴(3,4) and slope of altitude = 1

y - 4 = 1(x - 3)

y - 4 = x - 3

y = x - 3 + 4

y = x + 1

c) Bisector should cut the line into two equal parts, 

the right bisector of AC

𝐴(3, 4), 𝐵(−5, 2), and 𝐶(1, −4).

Midpoint of AC = (-5 + 1)/2, (4 - 4)/2

= -4/2, 0/2

Bisecting point of AC = D(-2, 0)

Slope of bisector of AC = -1/slope of of BD

= -1 / [(2-0) / (-5+2)]

= -1/(-2/3)

= 3/2

Equation of perpendicular bisector of AC :

y - 0 = 3/2(x + 2)

2y = 3(x + 2)

2y = 3x + 6

3x - 2y + 6 = 0

Related topics

• Find the coordinates of the point that divides the line segment into three parts
• How to find the ratio in which a point divides a line
• Midpoint of the line segment
• Section formula
• How to find the missing coordinate of a parallelogram

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.