HOW TO FIND THE MINIMUM OR MAXIMUM VALUE OF A FUNCTION IN VERTEX FORM

To find the vertex form of the parabola, we use the concept completing the square method.

Vertex form of a quadratic function :

y = a(x - h)² + k

In order to find the maximum or minimum value of quadratic function, we have to convert the given quadratic equation in the above form.

Minimum value of parabola :

If the parabola is open upward, then it will have minimum value

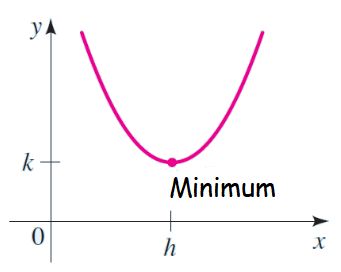
If a > 0, then minimum value of f is f(h)  =  k

Maximum value of parabola :

If the parabola is open downward, then it will have maximum value.

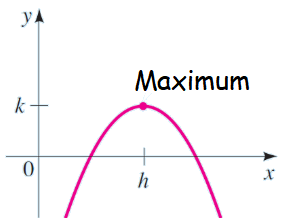
If a < 0, then maximum value of f is f(h)  =  k

Practice Problems

Problem 1 :

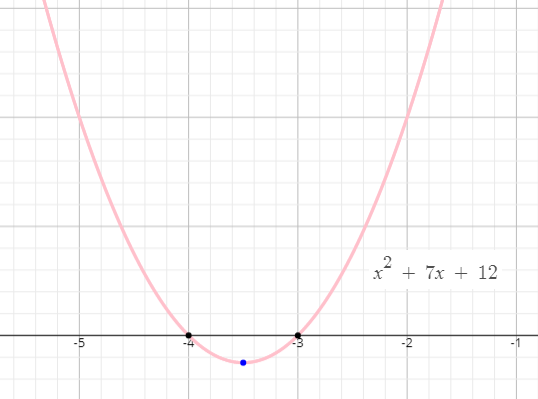
For the given function f(x) = x² + 7x + 12

(a) Write f(x) in the form k(x + t)² + r.

(b) Find the value of x where f(x) attains its minimum value or its maximum value.

(c) Find the vertex of the graph of f.

Solution :

Let y  =  x² + 7x + 12

y  =  x² + 2⋅x⋅(7/2) + (7/2)² - (7/2)² + 12

y  =  (x + (7/2))² + 12

By comparing it with vertex form, we get the value of k . Since it is positive, the parabola is open upward. So it will minimum value.

(b)  It has minimum value when x = -7/2

(c)  Vertex of the parabola is (-7/2, 12) 

Problem 2 :

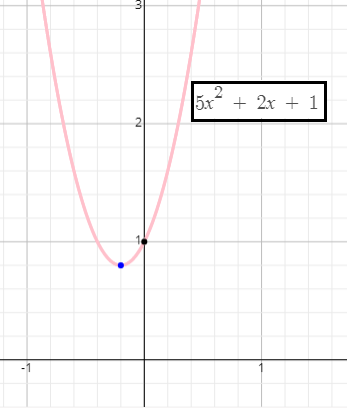
For the given function f(x) = 5x² + 2x + 1

(a) Write f(x) in the form k(x + t)² + r.

(b) Find the value of x where f(x) attains its minimum value or its maximum value.

(c) Find the vertex of the graph of f.

Solution :

Let y  =  5x² + 2x + 1

y  =  5(x² + x) + 1

y  =  5 [x² + 2 ⋅ x ⋅ (1/2) + (1/2)² - (1/2)²] + 1

y  =  5 [x + (1/2)]² - (1/4)] + 1

y  =  5 [x + (1/2)]² - (5/4) + 1

y  =  5 [x + (1/2)]² - (1/4) 

By comparing it with vertex form, we get the value of k . Since it is positive, the parabola is open upward. So it will minimum value.

(b)  It has minimum value when x = -1/2

(c)  Vertex of the parabola is (-1/2, -1/4) 

Problem 3 :

For the given function f(x) = −2x² + 5x − 2

(a) Write f(x) in the form k(x + t)² + r.

(b) Find the value of x where f(x) attains its minimum value or its maximum value.

(c) Find the vertex of the graph of f.

Solution :

Let y  = −2x² + 5x − 2

y  =   −2[x² - (5/2)x] − 2

y  =   −2[x² - (5/2)x] − 2

y  =  -2 [x² - 2 ⋅ x ⋅ (5/4) + (5/4)² - (5/4)²] - 2

y  =  -2 [x - (5/4)]² - (25/16)] - 2

y  =  -2 [x - (5/4)]² + (25/8) - 2

y  =  -2 [x - (5/4)]² + (9/8)

By comparing it with vertex form, we get the value of k . Since it is negative, the parabola is open downward. So it will maximum value.

(b)  It has maximum value when x = 5/4

(c)  Vertex of the parabola is (5/4, 9/8)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.