HOW TO FIND THE MISSING SIDE OF A RIGHT TRIANGLE USING SOHCAHTOA

Consider a right-angled triangle, right-angled at B.

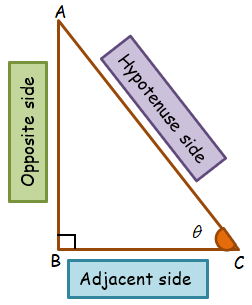
Formulas to find the six trigonometric ratios for a specific angle θ.

Examples 1-3 : Find the value of x. Round your answer to two decimal places.

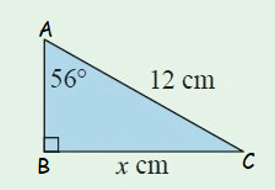
Example 1 :

Solution :

In the right triangle above, AC is the hypotenuse. Because the side AC is opposite to the right angle at B and its length 12 cm.

Considering the angle measure 56° at A, BC is the opposite side and its length is x cm.

We know the length of the hypotenuse and have to find the length of the opposite side.

Since the formula of sinθ contains opposite side and hypotenuse, we can use sinθ to find the length of the opposite side, that is the value of x.

Multiply both sides by 12.

9.95 ≈ x

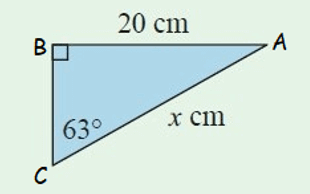
Example 2 :

Solution :

In the right triangle above, AC is the hypotenuse. Because the side AC is opposite to the right angle at B and its length is x cm.

Considering the angle measure 63° at C, AB is the opposite side and its length is 20 cm.

We know the length of the hypotenuse and have to find the length of the opposite side.

Since the formula of sinθ contains opposite side and hypotenuse, we can use sinθ to find the length of the opposite side, that is the value of x.

x ≈ 22.45

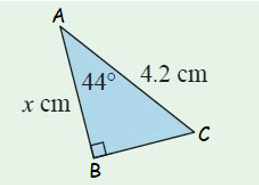
Example 3 :

Solution :

In the right triangle above, AC is the hypotenuse. Because the side AC is opposite to the right angle at B and its length is 4.2 cm.

Considering the angle measure 44° at A, AB is the adjacent side and its length is x cm.

We know the length of the hypotenuse and have to find the length of the adjacent side.

Since the formula of cosθ contains adjacent side and hypotenuse, we can use cosθ to find the length of the adjacent side, that is the value of x.

Multiply both sides by 12.

3.02 ≈ x

Examples 4-5 : Find the value of θ. Round your answer to the nearest integer.

Example 4 :

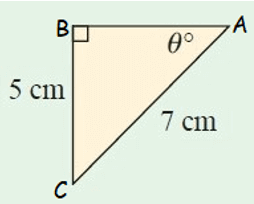
Solution :

In the right triangle above, AC is the hypotenuse. Because the side AC is opposite to the right angle at B and its length is 7 cm.

Considering the angle measure θ at A, BC is the opposite side and its length is 5 cm.

We know the lengths of the hypotenuse and opposite side and have to find the angle mesure θ.

Since the formula of sinθ contains opposite side and hypotenuse, we can use sinθ to find the angle measure θ.

sinθ = 0.7142.......

θ = sin^-1(0.7142.......)

θ ≈ 46°

Example 5 :

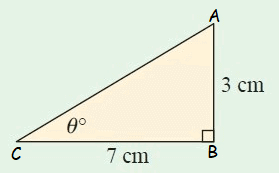
Solution :

In the right triangle above, considering the angle measure θ at C, AB is the opposite side with the length 3 cm and BC is the adjacent side with the length 7 cm.

We know the lengths of the opposite side and adjacent side and have to find the angle mesure θ.

Since the formula of tanθ contains opposite side and adjacent side, we can use tanθ to find the angle measure θ.

tanθ = 0.4285.......

θ = tan^-1(0.4285.......)

θ ≈ 23°

Example 6 :

Find the length of the shadow cast by a 1.8 m tall boy, when the sun is 72° above the horizon.

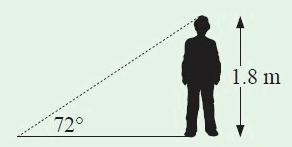
Solution :

The given situation forms a right triangle as shown below.

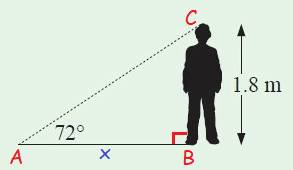
Here, x represents the length of the shadow of the boy.

In the right triangle above, considering the angle measure 72° at A, BC is the opposite side with the length 1.8 m and AB is the adcacent side with the length x m.

We know the length of the opposite side and adjacent side.

Since the formula of tanθ contains opposite side and adjacent side, we can use tanθ to find the length of the adjacent side, that is the value of x.

x ≈ 0.585 m

x = 0.585 ⋅ 100 cm

x = 58.5 cm

Therefore, the length of the shadow is about 58.5 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.