HOW TO FIND THE MISSING SIDE OF A RIGHT TRIANGLE

Example 1 :

Find the measure of each side indicated. Round to the nearest tenth.

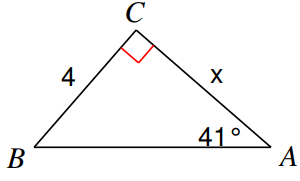
Solution :

Hypotenuse side  =  AB

Opposite side  =  BC   =  4

Adjacent side  =  AC  =  x

Here θ is 41°

The sides opposite and adjacent are involving in the trigonometric ratio tan θ

tan θ  =  Opposite side/Adjacent side  =  BC/AC

tan 41°  =  4/x

0.86  =  4/x

x =  4/0.86

  =  4.65

So, the measure of missing side is 4.6.

Example 2 :

Find the measure of each side indicated. Round to the nearest tenth.

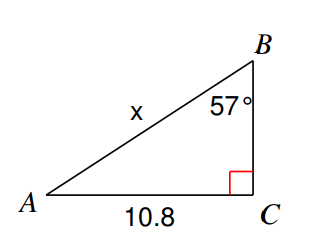
Solution :

Hypotenuse side  =  AB  =  x

Opposite side  =  AC   =  10.8

Adjacent side  =  BC

Here θ is 57°

The sides opposite and hypotenuse are involving in the trigonometric ratio sin θ

sin θ  =  Opposite side/Hypotenuse side  =  AC/AB

sin 57°  =  10.8/x

0.83  =  10.8/x

x =  10.8/0.83

  =  13.01

So, the measure of missing side is 13.

Example 3 :

Find the measure of each side indicated. Round to the nearest tenth.

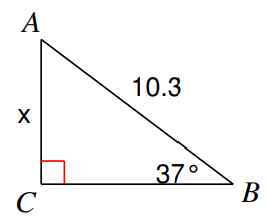
Solution :

Hypotenuse side  =  AB  =  10.3

Opposite side  =  AC   =  x

Adjacent side  =  BC

Here θ is 37°

The sides opposite and hypotenuse are involving in the trigonometric ratio sin θ

sin θ  =  Opposite side/Hypotenuse side  =  AC/AB

sin 37°  =  x/10.3

0.60  =  x/10.3

x =  10.3(0.60)

  =  6.18

So, the measure of missing side is 6.1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.