HOW TO FIND THE MISSING SIDE OF A TRIANGLE PRACTICE PROBLEMS

Find the value of x, giving your answer correct to 2 decimal places :

Problem 1 :

Solution

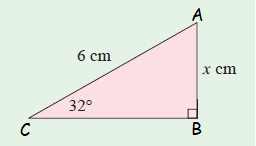
Problem 2 :

Solution

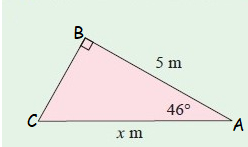
Problem 3 :

Solution

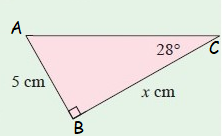
Problem 4 :

Solution

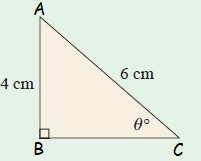
Problem 5 : 

Solution

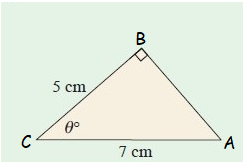
Problem 6 :

Solution

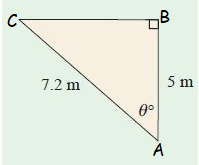
Problem 7 :

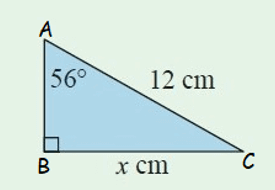
Solution

Problem 8 :

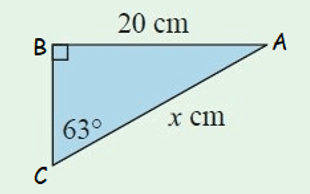
Solution

Problem 9 :

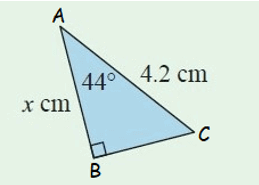
Solution

Problem 10 :

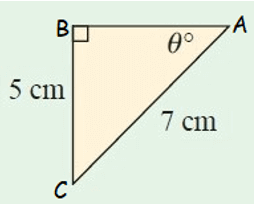
Solution

Problem 11 :

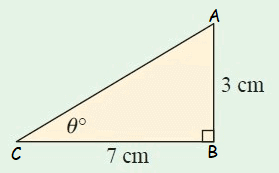
Solution

Problem 12 :

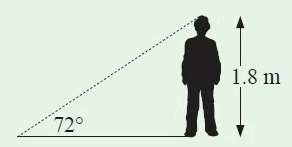
Solution

Answers

Problem 1 :

A guy wire is attached to a telephone pole 8 meter above the ground and it makes an angle of 50 degree with the ground. How long is the wire ?

Solution

Problem 2 :

When a child flying a kite has let out 50 m of string, the string makes an angle of 55 degree with the ground. How high is the kite ?

Solution

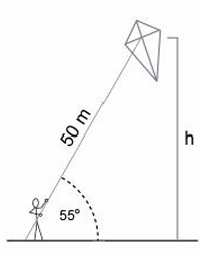
Problem 3 :

From P, the top of the building <APC and <BPC are measured as shown. The length of QB is 35 m, calculate AB, the height of building ?

Solution

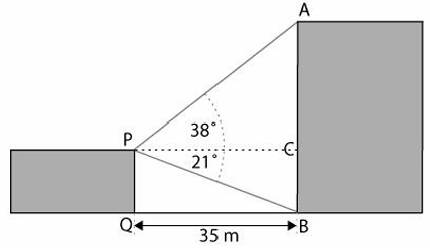
Problem 4 :

Given <ACB = 48, <D = 31 and AD = 56 cm find the length of AC.

Solution

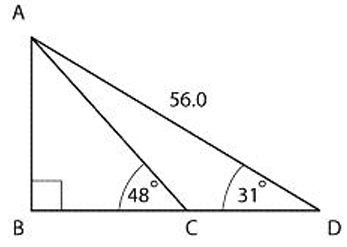
Problem 5 :

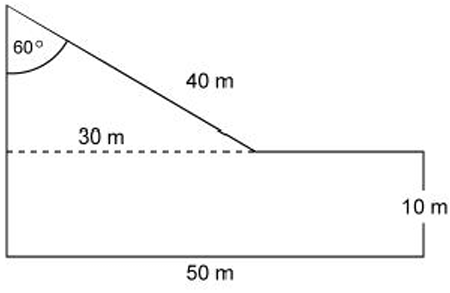
Calculate the area of the following plot of the land

Solution

Problem 1 :

A ramp for unloading a moving truck, has an angle of elevation of 30°. If the top of the ramp is 0.9 m above the ground level, then find the length of the ramp.

Solution

Problem 2 :

A girl of height 150 cm stands in front of a lamp-post and casts a shadow of length 150 √3 cm on the ground. Find the angle of elevation of the top of the lamp-post.

Solution

Problem 3 :

Suppose two insects A and B can hear each other up to a range of 2 m. The insect A is on the ground 1 m away from a wall and sees her friend B on the wall, about to be eaten by a spider. If A sounds a warning to B and if the angle of elevation of B from A is 30°, will the spider have a meal or not ? ( Assume that B escapes if she hears A calling )

Solution

Problem 4 :

Evelyn Granville, who is 1.5 m tall, is standing 20 m from the base of a building. She sights the top of the building with an angle of elevation of 58°. Find the height of the building.

Solution

Problem 5 :

A video camera is mounted on the top of a 120 m tall building. When it tilts down 36° from the horizontal, it views the base of another building. When it tilts up 47° from the horizontal, it views the top of the same building.

a) How far apart are the two buildings?

b) How tall is the building viewed by the camera?

Solution

Problem 6 :

A wind swept tree grows at an angle of 85 degree. An environmental scientist wants to know the height of the tree. She walks 50 m from the base of the tree and measures an angle of elevation of 40 degree to the top of the tree. How tall is the tree?

Solution

Problem 7 :

The lighthouse L is 5 km from the nearest point P on the shore. T is the tree further down the shoreline such that PT is perpendicular to PL. If <PLT = 37 degree, determine the distance from P to T.

Solution

Problem 1 :

A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45° . The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30° . Determine the speed at which the bird flies.(√3 = 1.732)

Solution

Problem 2 :

An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37° at a given point. After what period of time does the angle of elevation increase to 53° ? (tan 53° = 1.3270, tan 37° = 0.7536)

Solution

Problem 3 :

A bird is flying from A towards B at an angle of 35° , a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away.

(i) How far is B to the North of A?

(ii) How far is B to the West of A?

(iii) How far is C to the North of B?

(iv) How far is C to the East of B?

(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.