HOW TO FIND THE MISSING SIDES OF SIMILAR TRIANGLES

In geometry two triangles are similar if and only if corresponding angles are congruent and the lengths of corresponding sides are proportional.

Let us look at some examples to understand how to find the lengths of missing sides in similar triangles.

Example 1 :

Find the measures of the missing sides if  ΔKLM ∼ ΔNOP.

k  =  9, n  =  6, o  =  8, p  =  4

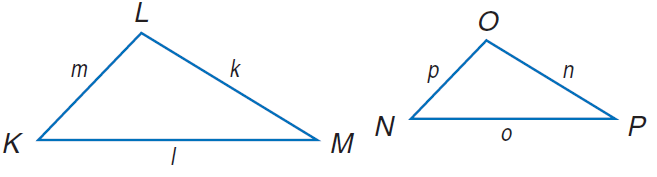
Solution :

Because the above triangles ΔKLM are ΔNOP similar, the ratios of the corresponding sides will be equal.

KL/NO  =  LM/OP   =  KM/NP

m/p  =  k/n  =  l/o

k  =  9, n  =  6, o  =  8, p  =  4

m/4  =  9/6  =  l/8

Example 2 :

Find the measures of the missing sides if  ΔKLM ∼ ΔNOP.

k  =  24, l  =  30, m  =  15, n  =  16

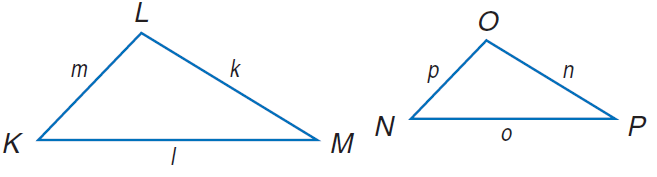
Solution :

Because the above triangles ΔKLM are ΔNOP similar, the ratios of the corresponding sides will be equal.

KL/NO  =  LM/OP   =  KM/NP

m/p  =  k/n  =  l/o

k  =  24, l  =  30, m  =  15, n  =  16

15/p  =  24/16  =  30/o

Example 3 :

Find the measures of the missing sides if  ΔKLM ∼ ΔNOP.

m  =  11, p  =  6, n  =  5, o  =  4

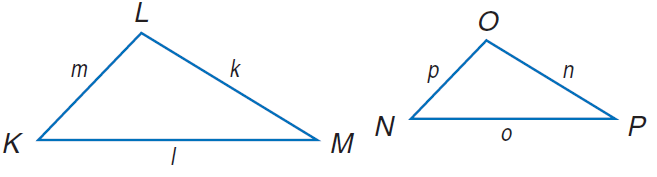
Solution :

Because the above triangles ΔKLM are ΔNOP similar, the ratios of the corresponding sides will be equal.

KL/NO  =  LM/OP  =  KM/NP

m/p  =  k/n  =  l/o

m  =  11, p  =  6, n  =  5, o  =  4

11/6  =  k/5  =  l/4

Example 4 :

Find the measures of the missing sides if ΔKLM ∼ ΔNOP.

k  =  16, l  =  13, m  =  12, o  =  7

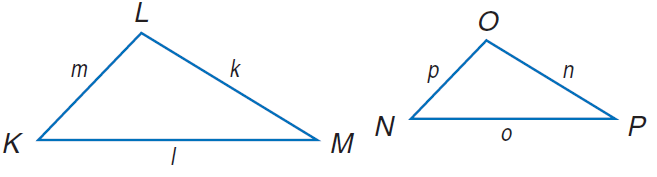
Solution :

Because the above triangles ΔKLM are ΔNOP similar, the ratios of the corresponding sides will be equal.

KL/NO  =  LM/OP   =  KM/NP

m/p  =  k/n  =  l/o

k  =  16, l  =  13, m  =  12, o  =  7

12/p  =  16/n  =  13/7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.