HOW TO FIND THE MISSING VALUE IN COMPOSITION OF TWO FUNCTIONS

Find the value of k, such that f o g = g o f.

Example 1 :

f(x) = 3x + 2 and g(x) = 6x - k

Solution :

f o g = g o f

f[g(x)] = g[f(x)]

f[6x - k] = g[3x + 2]

3(6x - k) + 2 = 6(3x + 2) - k

18x - 3k + 2 = 18x + 12 - k

Subtract 18x from each side. 

-3k + 2 = 12 - k

Add k to each side. 

-2k + 2 = 12

Subtract 2 from each side. 

-2k = 10

Divide each side by -2.

k = -5

Example 2 :

f(x) = 2x - k and g(x) = 4x + 5

Solution : 

f o g = g o f

f[g(x)] = g[f(x)]

f[4x + 5] = g[2x - k]

2(4x + 5) - k = 4(2x - k) + 5

8x + 10 - k = 8x - 4k + 5

Subtract 18x from each side. 

10 - k = -4k + 5

Add 4k to each side. 

10 + 3k = 5

Subtract 10 from each side. 

3k = -5

Divide each side by 3.

k = -5/3

Example 3 :

If f(x) = x² - 3x - 1 and g(x) = 1 - x, what is the value of (f o g)(-2)

A) -3    B) -1     C) 1     D) 3

Solution : 

f(x) = x² - 3x - 1 and g(x) = 1 - x

(f o g)(-2) = f[g(-2)]

Finding g(-2) :

g(-2) = 1 - (-2)

= 1 + 2

= 3

Applying the value of g(-2)

f[g(-2)] = f(3)

Applying x = 3 in the function f(x), we get

f(x) = x² - 3x - 1

f(3) = 3² - 3(3) - 1

= 9 - 9 - 1

(f o g)(-2) = -1

Example 4 :

If f(x) = (1 - 5x)/2 and g(x) = 2 - x, what is the value of f(g(3)) ?

A) -7     B) -2    C) 2      D) 3

Solution : 

Given that f(x) = (1 - 5x)/2 and g(x) = 2 - x

To find the value of f(g(3)), first we have to find g(3).

g(3) = 2 - 3

= -1

f(g(3)) = f(-1)

f(x) = (1 - 5x)/2

f(-1) = (1 - 5(-1))/2

= (1 + 5)/2

= 6/2

= 3

f(g(3)) = 3

Example 5 :

If f = {(-4, 12)(-2, 4) (2, 0) (3, 3/2)} and g = { (-2, 5) (0, 1) (4, -7) (5, -9) }, what is the value of (g o f) (2)

A) -9     B) -7    C) 1      D) 5

Solution : 

f = {(-4, 12)(-2, 4) (2, 0) (3, 3/2)} and g = { (-2, 5) (0, 1) (4, -7) (5, -9) }

(g o f) (2) = g[f(2)]

From the ordered pairs of f, we know that

f(2) = 0

Applying the value of f(2), we get

= g[0]

= 1

(g o f) (2) = 1

Example 6 :

The function f satisfies f(-1) = 8 and f(1) = -2. A function g(2) satisfies g(2) = 5 and g(-1) = 1, what is the value of f(g(-1))

A) -9     B) -7    C) 1      D) 5

Solution : 

Given that f(-1) = 8, f(1) = -2, g(2) = 5, g(-1) = 1

f(g(-1)) = f(1)

= 2

So, the value of f(g(-1)) is 2

Example 7 :

g(x) = ax² + 24

for the function g defined above, a is constant  and g(4) = 8, what is the value of g(-4) ?

a)  8   b)  0   c)  -1    d)  -8

Solution :

g(x) = ax² + 24 -----(1)

g(4) = a(4)² + 24

8 = 16a + 24

8 - 24 = 16a

-16 = 16a 

a = -1

Applying a = -1 in (1), we get

g(x) = -x² + 24

g(-4) = -(-4)² + 24

= -16 + 24

= 8

So, option a is correct.

Example 8 :

If f(x) = √x + 2 and g(x) = -(x - 1)², which of the following is equivalent to g(f(a)) - 2f(a) ?

Solution :

f(x) = √x + 2 and g(x) = -(x - 1)²

g(f(a)) = g(√a + 2)

g(√a + 2) = -((√a + 2) - 1)²

= -(√a + 2 - 1)²

= -(√a + 1)²

= - (a + 2√a + 1)

= -a - 2√a - 1

2f(a) = 2(√a + 2)

= 2√a + 2

g(f(a)) - 2f(a) = - a - 2√a - 1 - (2√a + 2)

= -a - 2√a - 1 - 2√a - 2

= -a - 4√a - 3

Example 9 :

The table above gives values of f and g at selected values of x. What is the value of g(f(2)) ?

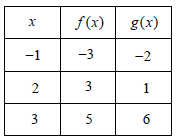
Solution :

Evaluating g(f(2)) :

From the table, for input x = 2

= g(3)

= 6

So, the value of g(f(2)) is 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.