HOW TO FIND THE NUMBER OF ELEMENTS IN A MATRIX
Question 1 :
In the matrix A =
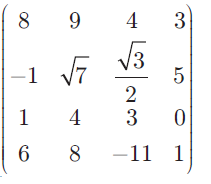
write (i) The number of elements
(ii) The order of the matrix
(iii) Write the elements a22, a23 , a24 , a34, a43 , a44.
Solution :
(i) In the given matrix, we have 4 rows and 4 columns.
Hence the number of elements in the given matrix is 16.
(ii) The order of matrix is 4 x 4.
(iii) a22 means the element is in place 2nd row and second column.
a22 = √7
a23 = √3/2 (Element at the 2nd row and 3rd column)
a24 = 5 (Element at the 2nd row and 4th column)
a34 = 0 (Element at the 3rd row and 4th column)
a43 = -11 (Element at the 4th row and 3rd column)
a44 = 1 (Element at the 4th row and 4th column)
Question 2 :
If a matrix has 18 elements, what are the possible orders it can have? What if it has 6 elements?
Solution :
Possible orders of matrices having 18 elements are 1 x 18, 18 x 1, 6 x 3, 3 x 6 , 2 x 9, 9 x 2.
Possible orders of matrices having 6 elements are 1 x 6, 6 x 1, 2 x 3, 3 x 2.
How to Construct a Matrix with Given aij
Question 3 :
Construct a 3 x 3 matrix whose elements are given by
(i) aij = |i - 2j|
Solution :
Number of rows of the required matrix is 3.
Number of columns of the required matrix is 3.
|
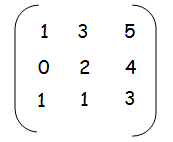
aij = |i - 2j| a11 = |1 - 2(1)| = |1 - 2| a11 = 1 |
aij = |i - 2j| a12 = |1 - 2(2)| = |1 - 4| a12 = 3 |
aij = |i - 2j| a13 = |1 - 2(3)| = |1 - 6| a11 = 5 |
|
a21 = |2 - 2(1)| = |2 - 2| a21 = 0 |
a22 = |2 - 2(2)| = |2 - 4| a22 = 2 |
a23 = |2- 2(3)| = |2 - 6| a23 = 4 |
|
a31 = |3 - 2(1)| = |3 - 2| a31 = 1 |
a32 = |3 - 2(2)| = |3 - 4| a32 = 1 |
a33 = |3- 2(3)| = |3 - 6| a33 = 3 |
Hence the required matrix is A =
(ii) aij = (i + j)3/3
Solution :
|
aij = (i + j)3/3 a11 = (1+1)3/3 = 23/3 a11 = 8/3 |
aij = (i + j)3/3 a12 = (1+2)3/3 = 27/3 a12 = 9 |
aij = (i + j)3/3 a13 = (1+3)3/3 a13 = 64/3 |
|
a21 = (2+1)3/3 = 27/3 a21 = 9 |
a22 = (2+2)3/3 = 64/3 a22 = 64/3 |
a23 = (2+3)3/3 a23 = 125/3 |
|
a31 = (3+1)3/3 = 64/3 a31 = 64/3 |
a32 = (3+2)3/3 = 125/3 a32 = 125/3 |
a33 = (3+3)3/3 a33 = 216/3 |
Hence the required matrix is

Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

