HOW TO FIND THE PRODUCT OF TWO MATRICES

How to Find the Product of Two Matrices ?

Here we are going to see some example problems based on finding product of two matrices.

How to Find the Product of Two Matrices - Questions

Question 1 :

If 

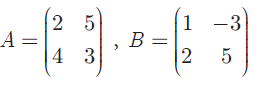
find AB, BA and check if AB = BA? 

Solution :

AB  =  

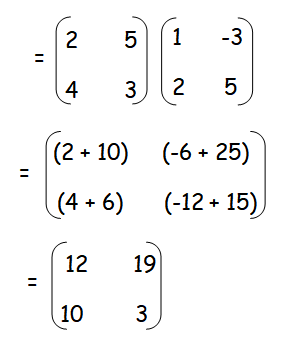
BA  =  

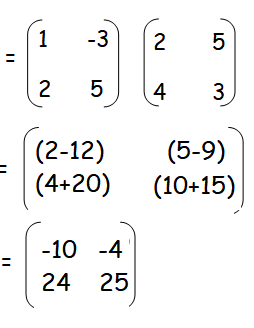
AB and BA are not equal.

Question 2 :

Given that

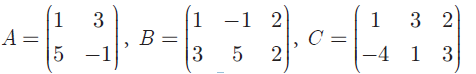
verify that A(B + C) = AB + AC .

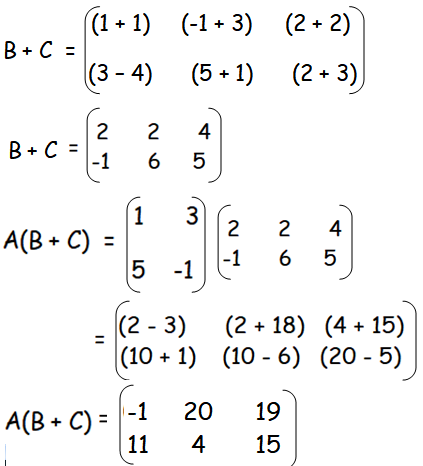
R.H.S :

AB  =

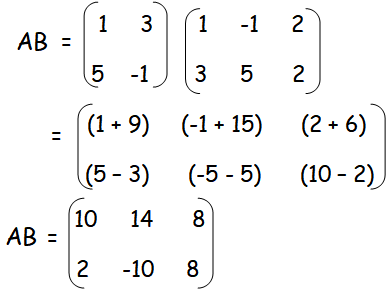
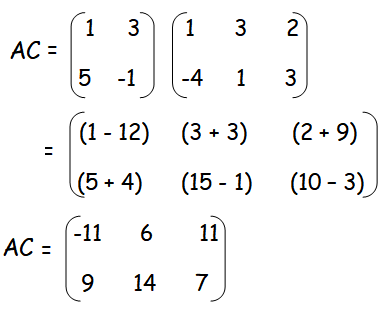
Now, let us add AB and AC

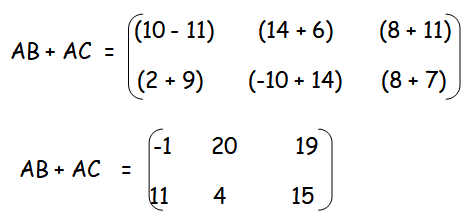
 Hence proved.

Question 3 :

Show that the matrices

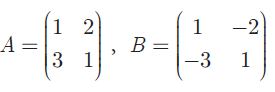
satisfy commutative property AB = BA

Solution :

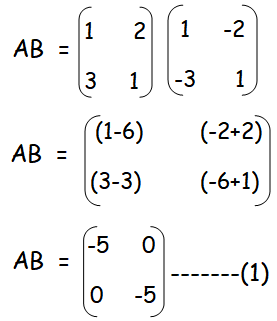
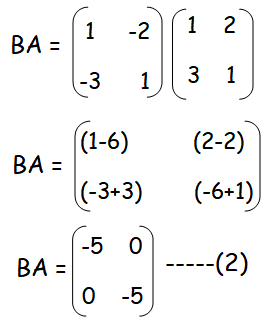
Hence the commutative property is true for the above matrices.

Question 4 :

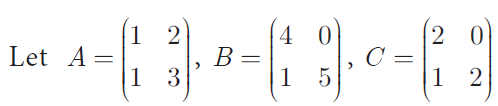
Show that (i) A(BC) = (AB)C

(ii) (A−B)C = AC −BC (iii) (A−B)^T = A^T −B^T

Solution :

(i) A(BC) = (AB)C

First let us find the product of B and C.

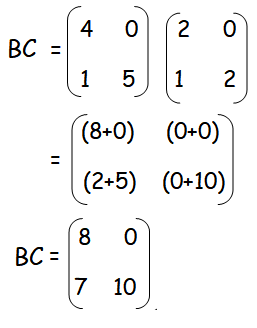
Let us multiply the matrices A and BC.

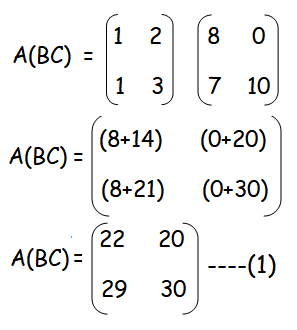
Let us find the product of AB.

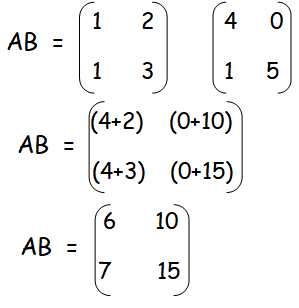
Multiplying the matrices AB and , we get

A(BC)  =  (AB)C

Hence it is proved.

(ii) (A−B)C = AC −BC 

Solution :

L.H.S

(A−B) C  =  

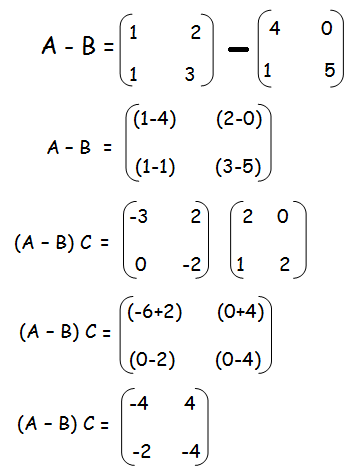
R.H.S :

AC  =  

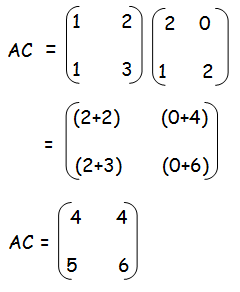
BC  =  

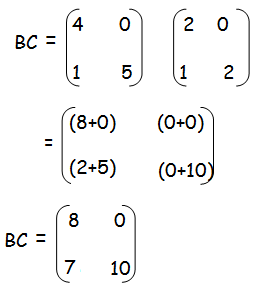
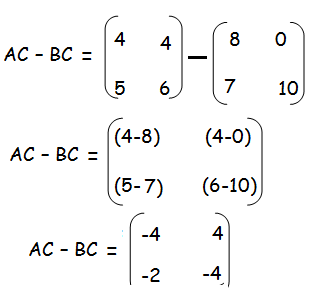
(A−B)C = AC −BC 

(iii) (A−B)^T = A^T −B^T

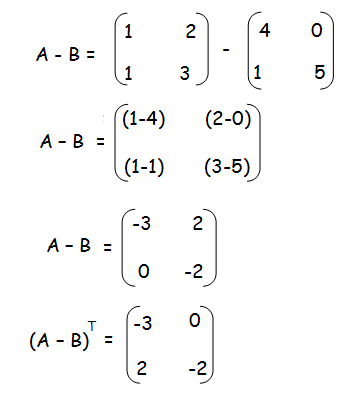
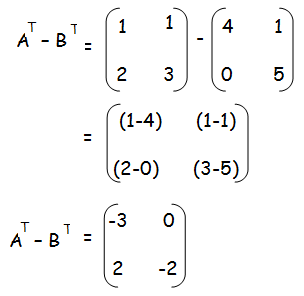
Hence proved.

Question 5 :

If

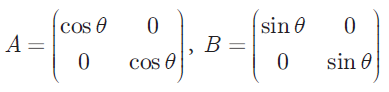
then show that A² +B² = I .

Solution :

A²   =  A x A

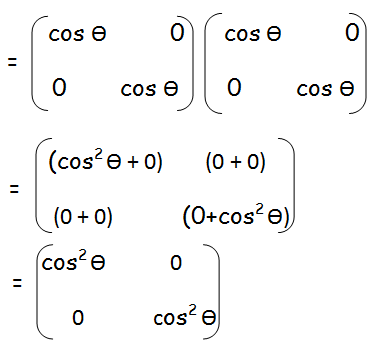
B²  =  B x B

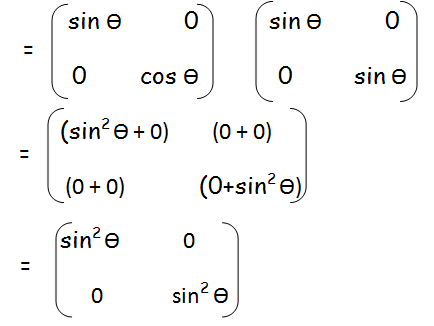
By adding the corresponding terms, we get 

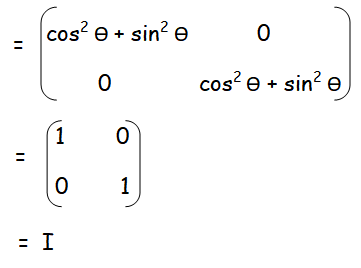
Hence proved.

Question 6 :

If A = 

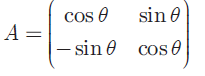
prove that AA^T = I .

Solution :

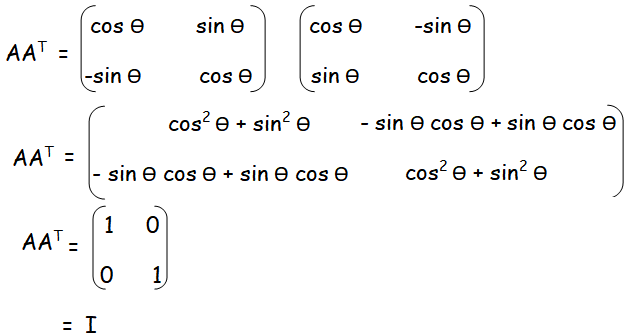
Question 7 :

Verify that A² = I when

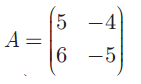
Solution :

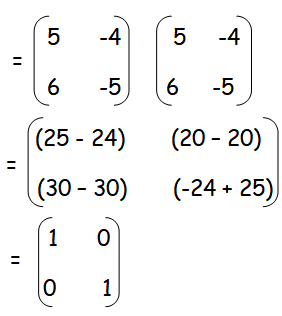
  =  I  (hence proved)

Question 8 :

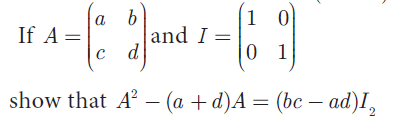
Solution :

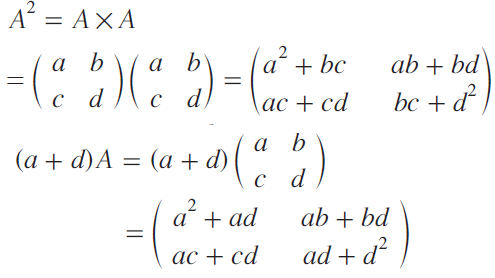
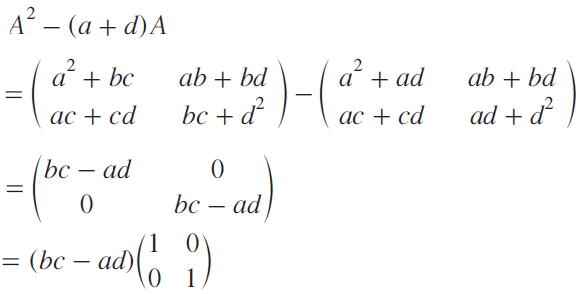
Question 9 :

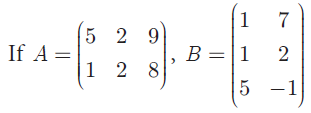
verify that (AB)^T = B^TA^T

Solution :

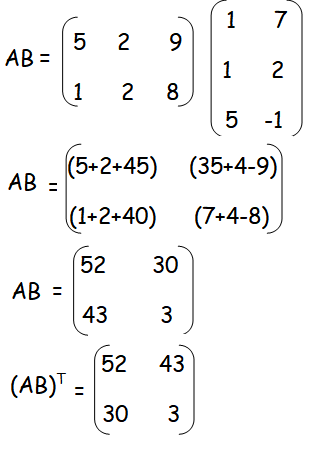
Question 10 :

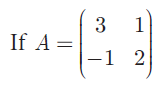
show that A² - 5A + 7I₂  =  0

Solution :

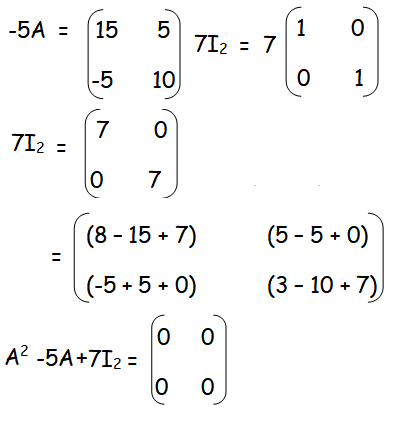
Hence proved.

After having gone through the stuff given above, we hope that the students would have understood, "How to Find the Product of Two Matrices". 

Apart from the stuff given in this section "How to Find the Product of Two Matrices", if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.