HOW TO FIND THE QUOTIENT WHEN DIVIDING POLYNOMIALS

Question 1

Find the quotient and remainder using synthetic division.

(x³ + x² - 3 x + 5 ) ÷ ( x - 1 ) 

Solution :

Let p(x) = x³ + x² - 3x + 5 and q(x) = x - 1. We can find the quotient s(x) and the remainder r, by proceeding as follows.

q(x)  =  0

x - 1  =  0

x  =  1

Step 1 :

Arrange the dividend and the divisor according to the descending powers of x and then write the coefficients of dividend in the first zero. Insert 0 for missing terms.

Step 2 :

Find out the zero of the divisor.

Step 3 :

Put 0 for the first entry in the second row. 

Step 4 :

Write down the quotient and remainder accordingly. All the entries except the last one  in the third row constitute the coefficients of the quotient. 

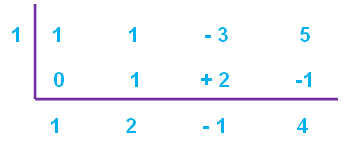
When P(x) is divided by (x - 1),

Quotient = x² + 2 x - 1

Remainder = 4

Question 2 :

Find the quotient and remainder using synthetic division

(3x³ - 2x² + 7 x - 5) ÷ (x + 3)

Solution :

Let p (x) = 3x³ - 2x² + 7 x - 5 be the dividend and q (x) = x + 3 be the divisor. We shall find the quotient s(x) and the remainder r, by proceeding as follows.

q(x) = 0

x + 3 = 0

     x = - 3

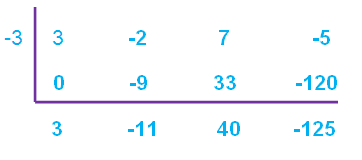
When P (x) is divided by (x + 3), the quotient is 3 x² - 11 x + 40 and the remainder is - 125.

Quotient = 3x² - 11 x + 40

Remainder = - 125

When we want to divide a given polynomial by another polynomial, first we have to write the dividend inside the long division sign from highest degree to lowest degree.

For example, the highest degree of the polynomial is 3, then the next term of the dividend must be the square term and so on. In this, if we don't have square term, we have to write 0 instead of that and we can write the next term.

Let us see some example problems based on the above concept.

Question 3 :

Find (a³ + 8a - 24) ÷ (a - 2)

Solution :

The degree of the given polynomial is 3 then we must have square term. But here we don't have square term, so we have to replace it by 0.

Step 1 :

In the first step, we have to divide the first term of the dividend by the first term of the divisor.

If we divide a³ by a, we will get a². We have to write a² at the top and multiply each term of the dividend by a².

a²(a - 2)  =  a³ -  2a²

By subtracting a³ -  2a² from (a³ + 8a - 24), we get 2a² + 8a + 24.

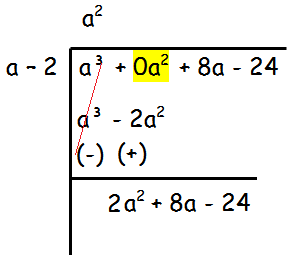
Step 2 :

Now we have to divide 2a² by a, so we will get 2a.

• By multiplying this 2a by (a - 2), we get 2a² - 4a.
• By subtracting 2a² - 4a from 2a² - 8a - 24, we get 12a - 24

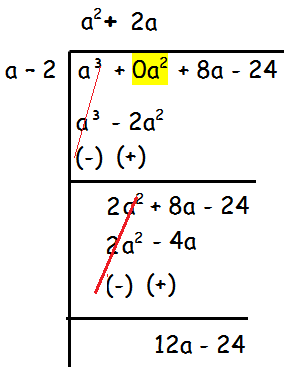
Step 3 :

Divide 12a by a, so we get 12.

• By multiplying this 12 by (a - 2), we get 12a - 24.
• By subtracting 12a - 24 from 12a - 24, we get 0.

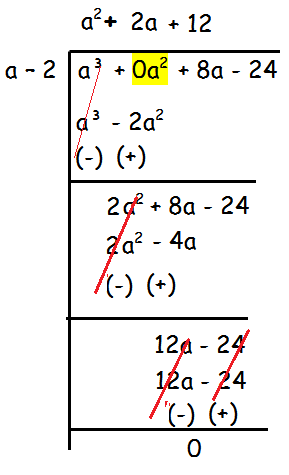
Hence, 

Quotient  =  a² + 2a + 12

Remainder  =  0

Question 4 :

Find (4x³ + 2x² - 5)  ÷ 2x

Solution :

The degree of the given polynomial is 3. But here we don't have x term, so we have to replace it by 0.

Step 1 :

In the first step, we have to divide the first term of the dividend by the first term of the divisor.

If we divide 4x³ by 2x, we will get 2x².

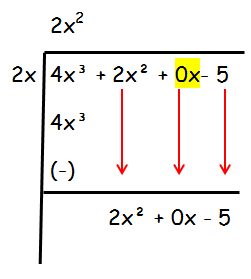Step 2 :

Now we have to divide the first term of the dividend 2x² by 2x, so we get x.

• By multiplying x by 2x, we get 2x³.
• Subtracting 2x² form 2x²,  we get 0
• Bring down the next term, we get -5

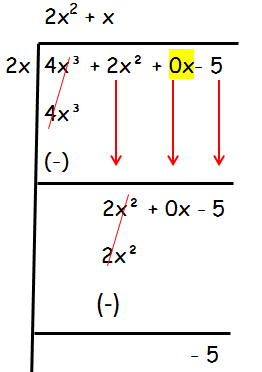
Hence, 

Quotient  =  2x² + x

Remainder  =  -5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.