HOW TO FIND THE VERTICES OF A TRIANGLE IF THE MIDPOINTS ARE GIVEN
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Let D(x1, y1), E(x2, y2) and C(x3, y3) be the mid points of the sides AB, BC and CA of ΔABC.
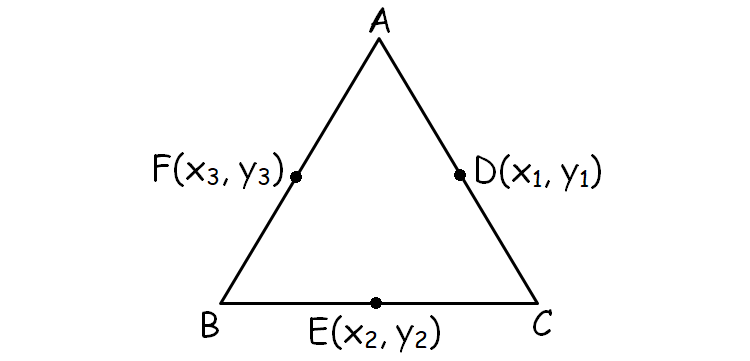
Then, the vertices of ΔABC can be found as shown below.
A(x1 + x3 - x2, y1 + y3 - y2)
B(x1 + x2 - x3, y1 + y2 - y3)
C(x2 + x3 - x1, y2 + y3 - y1)
Example 1 :
The mid-points of the sides of a triangle are (5, 1), (3, -5) and (-5, -1). Find the coordinates of the vertices of the triangle.
Solution :
Let D, E and F be the mid points of the sides AB, BC and CA of ΔABC.
D(x1, y1) = (5, 1)
E(x2, y2) = (3, -5)
F(x3, y3) = (-5, -1)
Vertex A :
A(x1 + x3 - x2, y1 + y3 - y2)
A(5 - 5 - 3, 1 - 1 - (-5))
A(-3, 5)
Vertex B :
B(x1 + x2 - x3, y1 + y2 - y3)
B(5 + 3 - (-5), 1 - 5 - (-1))
B(8 + 5, 1 - 5 + 1)
B(13, -3)
Vertex C :
C(x2 + x3 - x1, y2 + y3 - y1)
C(3 - 5 - 5, -5 - 1 - 1)
C(3 - 10, -5 - 2)
C(-7, -7)
Example 2 :
The mid-points of the sides of a triangle are (5, 3), (4, 0) and (2, 2). Find the coordinates of the vertices of the triangle.
Solution :
Let D, E and F be the mid points of the sides AB, BC and CA of ΔABC.
D(x1, y1) = (5, 3)
E(x2, y2) = (4, 0)
F(x3, y3) = (2, 2)
Vertex A :
A(x1 + x3 - x2, y1 + y3 - y2)
A(5 + 2 - 4, 3 + 2 - 0)
A(3, 5)
Vertex B :
B(x1 + x2 - x3, y1 + y2 - y3)
B(5 + 4 - 2, 3 + 0 - 2)
B(7, 1)
Vertex C :
C(x2 + x3 - x1, y2 + y3 - y1)
C(4 + 2 - 5, 0 + 2 - 3)
C(1, -1)
Example 3 :
If 𝐴(4, 2),𝐵(7, 6) and 𝐶(1, 4) are the vertices of a ∆ 𝐴𝐵𝐶 and 𝐴𝐷 is its median, prove that the median 𝐴𝐷 divides ∆ 𝐴𝐵𝐶 into two triangles of equal areas.
Solution :
Here D is the midpoint of the side BC.
Midpoint = (x1 + x2)/2, (y1 + y2)/2
= (7 + 1)/2, (6 + 4)/2
= 8/2, 10/2
= D(4, 5)
Now we are finding out the area created by the vertices ABD and ACD.
Distance between A and D = height of the triangle
d = √[(x2 - x1)2 + (y2 - y1)2]
A(4, 2) D(4, 5)
= √[(4 - 4)2 + (5 - 2)2]
= √[02 + 32]
= 3
Height of the triangle = 3 units
Since AD is the median, it will bisect the opposite side into two halves.
B(7, 6) D(4, 5)
Distance between BD
= √[(4 - 7)2 + (5 - 6)2]
= √[32 + (-1)2]
= √10
Base of the triangle = √10 units
Area of the triangle = (1/2) x base x height
= (1/2) x 3 x √10
= 1.5 √10 square units
Distance between CD
𝐶(1, 4) and D(4, 5)
= √[(4 - 1)2 + (5 - 4)2]
= √[32 + 12]
= √9 + 1
= √10
Base of the triangle = √10 units
Area of triangle ACD = (1/2) x CD x AD
= 1/2 x √10 x 3
= 1.5 √10 square units.
So, median is dividing the triangle into equal triangles consisting of same area.
Example 4 :
𝐴(4, −6),𝐵(3, −2) and 𝐶(5, 2) are the vertices of a ∆ 𝐴𝐵𝐶 and 𝐴𝐷 is its median. Prove that the median 𝐴𝐷 divides ∆𝐴𝐵𝐶 into two triangles of equal areas.
Solution :
Here D is the midpoint of the side BC.
Midpoint = (x1 + x2)/2, (y1 + y2)/2
= (3 + 5)/2, (-2 + 2)/2
= 8/2, 0/2
= D(4, 0)
Now we are finding out the area created by the vertices ABD and ACD.
Distance between A and D = height of the triangle
d = √[(x2 - x1)2 + (y2 - y1)2]
A(4, -6) D(4, 0)
= √[(4 - 4)2 + (0 + 6)2]
= √[02 + 62]
= 6
Height of the triangle = 6 units
Since AD is the median, it will bisect the opposite side into two halves.
B(3, -2) D(4, 0)
Distance between BD
= √[(4 - 3)2 + (0 + 2)2]
= √[12 + 22]
= √5
Base of the triangle = √5 units
Area of the triangle = (1/2) x base x height
= (1/2) x 6 x √5
= 3 √5 square units
Distance between CD
𝐶(5, 2) and D(4, 0)
= √[(4 - 5)2 + (0 - 2)2]
= √[12 + (-2)2]
= √1 + 4
= √5
Base of the triangle = √5 units
Area of triangle ACD = (1/2) x CD x AD
= 1/2 x 6 x √5
= 3 √5 square units.
So, median is dividing the triangle into equal triangles consisting of same area.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

