HOW TO FIND VECTOR PRODUCT OR CROSS PRODUCT OF TWO VECTORS

Working rule to find the cross product

Let 

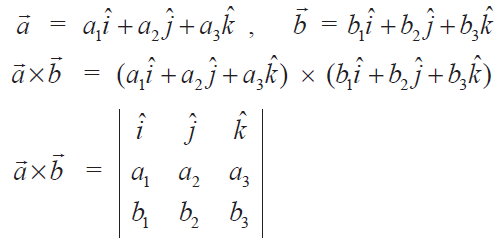
Finding cross product of two vectors  - Examples

Question 1 :

Find the magnitude of a vector x b vector, if a vector  =  2i vector + j vector + 3k vector and b vector  =  3i vector+ 5j vector - 2k vector

Solution :

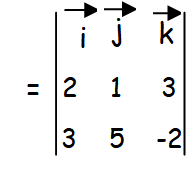
  =  i vector[-2 - 15] - j vector[-4 -9] + k vector[10-3]

  =  i vector[-17] - j vector[-13] + k vector[7]

a x b  =  -17 i vector + 13 j vector + 7 k vector

In order to find its magnitude, we have to take square root and find the sum of coefficients of i, j and k.

|a x b|  =  √(-17)² + 13² + 7²

  =  √(289 + 169 + 49)

  =  √507

Question 2 :

Show that 

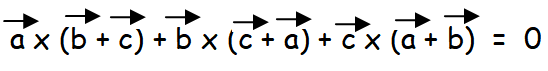
Solution :

a x (b + c)  =  a x b + a x c  ---(1)

b x (c + a)  =  b x c + b x a  ---(2)

c x (a + b)  =  c x a + c x b  ---(3)

(1) + (2) + (3)

a x (b + c) + b x (c + a) + c x (a + b) 

=  a x b + a x c + b x c + b x a + c x a + c x b

Since commutative property is not applicable in cross product,

  =  a x b + a x c + b x c - a x b - a x c - b x c

  =  0

Hence it is proved.

Question 3 :

Find the vectors of magnitude 10√3 that are  perpendicular to the plane which contains i vector + 2j vector + k vector and i vector + 3j vector + 4k vector

Solution :

Let a vector  =  i vector + 2j vector + k vector

b vector  =  i vector + 3j vector + 4k vector

required vector perpendicular to given vectors 

=  ± μ [(a x b)/ |a x b|]

  =  i[8-3] - j[4-1] + k[3-2]

a x b  =  5i - 3j + k

|a x b|  =  √5² + (-3)² + 1²

  =  √(25+9+1)

  =  √35

Required vector  = ± (10√3/√35) (5i - 3j + k)

= ± (10√3/√35) (5i - 3j + k)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.