HOW TO FIND WHICH TRIGONOMETRIC ANGLES HAVE POSITIVE OR NEGATIVE

Example 1 :

Without using a calculator, state whether each ratio is positive or negative.

(a) sin155°

Solution :

The given angle lies between 90 < θ < 180, that is 155 lies in 2nd quadrant. Hence sin 155 will have positive sign.

b) cos320°

Solution :

The given angle lies between 270 < θ < 360, that is 320 lies in 4th quadrant. Hence cos 320 will have positive sign.

c) tan120°

Solution :

The given angle lies between 90 < θ < 180, that is 120 lies in 2nd quadrant. Hence tan 120 will have negative sign.

d) cos220°

Solution :

The given angle lies between 180 < θ < 270, that is 220 lies in 3rd quadrant. Hence cos 220 will have negative sign.

Example 2 :

An angle is in standard position such that sin θ = 5/13.

a) Sketch a diagram to show the two possible positions of the angle. 

b) Determine the possible values of θ, to the nearest degree, if 0° ≤ θ < 360°.

Solution :

sin θ = 5/13  =  Opposite side / Hypotenuse side

Adjacent side  =  √13² - 5²  =  √144  =  12

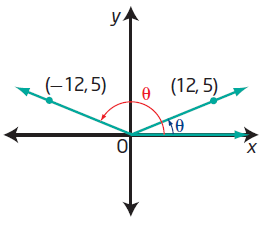
If the terminal side is in 1st quadrant, then sin θ = 5/13. So, the required angle will be 23.

If the terminal side is in 2nd quadrant, the angle will be 180 - 23. That is 157.

Finding Other Two Primary Trigonometric Ratios If One Ratio is Given

Example :

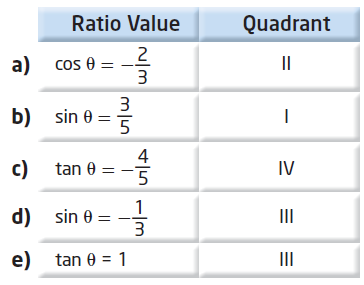
An angle in standard position has its terminal arm in the stated quadrant. Determine the exact values for the other two primary trigonometric ratios for each.

Solution :

(a) cosθ = -2/3. Since the terminal side lies in 2nd quadrant only sin θ and cosec θ will have positive sign.

So sin θ  =  Opposite side / Hypotenuse side

Opposite side  =  √3² - (-2)²

 =  √9 - 4  =  √5

Solution :

(b) sinθ = 3/5. Since the terminal side lies in 1st quadrant all trigonometric angles will have positive sign.

So sin θ  =  Opposite side / Hypotenuse side  =  3/5

Adjacent side  =  √5² - 3²

 =  √25 - 9  =  √16  =  4

cos θ  =  4/5

tan θ  =  3/4

Solution :

(c) tanθ = -4/5. Since the terminal side lies in 4th quadrant cos θ and sec θ will have positive sign.

So tan θ  =  Opposite side / Adjacent side  =  -4/5

Hypotenuse side  =  √5² + 4²

 =  √25 + 16  =  √41

sin θ  =  -4/√41

cos θ  =  5/√41

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.