HOW TO FIND X INTERCEPT OF A FUNCTION

Examples 1-3 : Find the x-intercept of the function, sketch the graph and verify it.

Example 1 :

y = 2x - 3

Solution :

y = 2x - 3

Substitute y = 0 to find the x-intercept.

2x - 3 = 0

Add 3 to both sides.

2x = 3

Divide both sides by 2.

x = 1.5

The given function has one x-intercept and it is 1.5.

Sketch the Graph :

The given function is linear and it is slope-intercept form. That is y = mx + b.

Comparing y = mx + b and y = 2x -3,

slope m = 2

y-intercept b = 3

The y-intercept is 3, so we plot a point at -1 on the y-axis to begin.

We know that the slope is equal to rise over run.

slope = rise/run

2 = 2/1

rise = 2 and run = 1

Since the slope is positive we’ll move up two and right one to plot the next point.

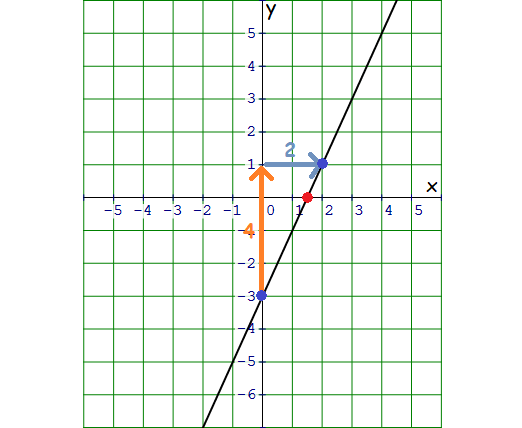
In the graph above, the line intersects the x-axis at 1.5.

Example 2 :

y = x² - x - 6

Solution :

Substitute y = 0 to find the x-intercept.

x² - x - 6 = 0

Solve by factoring.

In the quadratic equation above, the coefficient of x² is 1. So, get two factors of the constant term '-6' such that the sum of the two factors is equal to the coefficient of x, that is '-1'.

Then the two factors of '-6' are '+2' and '-3'.

Now, split the middle term -6x using the two factors -3 and -3.

x² - x - 6 = 0

x² + 2x - 3x - 6 = 0

x(x + 2) - 3(x + 2) = 0

(x + 2)(x - 3) = 0

x + 2 = 0  or  x - 3 = 0

x = -2  or  x = 3

The given function has two x-intercepts and they are -2 and 3.

Graphing :

Comparing y = ax² + bx + c and y = x² - x - 6,

a = 1, b = -1 and c = -6

a = 1 > 0 ----> parabola opens up

x-coordinate of the vertex :

x = -b/2a

Substitute a = 1 and b = -1.

x = -(-1)/2(1)

x = 1/2

x = 0.5

y-coordinate of the vertex :

Substitute x = 0.5 in y = x² - x - 6.

y = (0.5)² - (0.5) - 6

= 0.25 - 0.5 - 6

= -6.25

Vertex of the parabola is (0.5, -6.25).

Take some random values for x and find the corresponding values of y.

If x = -1,

y = (-1)² - (-1) - 6

= 1 + 1 - 6

= -4

(-1, -4)

If x = 0,

y = 0² - 0 - 6

= -6

(0, -6)

If x = 1,

y = 1² - 1 - 6

= 1 - 1 - 6

= -6

(1, -6)

If x = 2,

y = 2² - 2 - 6

= 4 - 2 - 6

= -4

(2, -4)

The given function is quadratic and its graph is a parabola. The parabola opens up with the vertex (0.5, -6.25).

Plot the points (-1, -4), (0, -6), (1, -6) and (2, -4) and sketch the graph of the parabola.

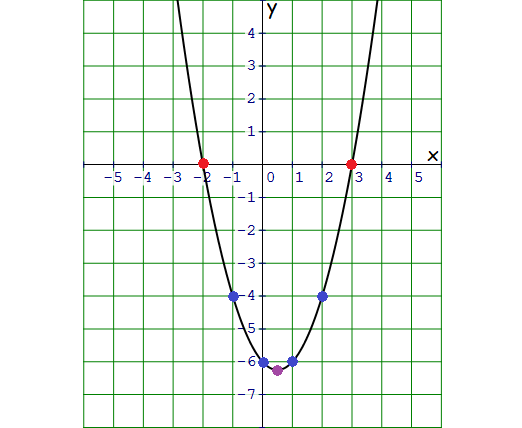
In the graph above, the parabola intersects the x-axis at -2 and 3.

Example 3 :

y = x² - 4x + 7

Solution :

Substitute y = 0 to find the x-intercept.

x² - 4x + 7 = 0

Solve by factoring.

In the quadratic equation above, the coefficient of x² is 1. So, get two factors of the constant term '+7' such that the sum of the two factors is equal to the coefficient of x, that is '-4'.

We can not get such two factors. So, the quadratic equation x² - 4x + 7 = 0 can not be solved by factoring.

So, we can use quadratic formula to solve it.

Comparing ax² + bx + c = 0 and x² - x + 7 = 0,

a = 1, b = -1 and c = 7

The above two values of x are imaginary. So, the given function has no x-intercept.

Graphing :

Comparing y = ax² + bx + c and y = x² - 4x + 7,

a = 1, b = -4 and c = 7

a = 1 > 0 ----> parabola opens up

x-coordinate of the vertex :

x = -b/2a

Substitute a = 1 and b = -4.

x = -(-4)/2(1)

x = 4/2

x = 2

y-coordinate of the vertex :

Substitute x = 2 in y = x² - 4x + 7.

y = 2² - 4(2) + 7

= 4 - 8 + 7

= 3

Vertex of the parabola is (2, 3).

Take some random values for x and find the corresponding values of y.

If x = 0,

y = 0² - 4(0) + 7

= 7

(0, 7)

If x = 1,

y = 1² - 4(1) + 7

= 1 - 4 + 7

= 4

(1, 4)

If x = 3,

y = 3² - 4(3) + 7

= 9 - 12 + 7

= 4

(3, 4)

If x = 4,

y = 4² - 4(4) + 7

= 16 - 16 + 7

= 7

(4, 7)

The given function is quadratic and its graph is a parabola. The parabola opens up with the vertex (2, 3).

Plot the points (0, 7), (1, 4), (3, 4) and (4, 7) and sketch the graph of the parabola.

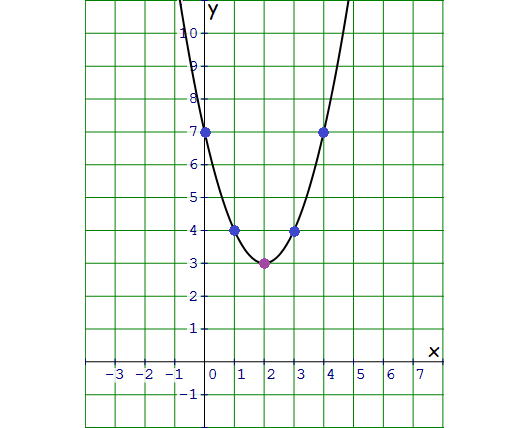
In the graph above, the parabola does not intersect the x-axis.

Examples 4-6 : Find the x-intercept of the function.

Example 4 :

y = x³ - 3x² - 4x + 12

Solution :

y = x³ - 3x² - 4x + 12

Substitute y = 0 to find the x-intercept.

x³ - 3x² - 4x + 12 = 0

x²(x - 3) - 4(x - 3) = 0

(x - 3)(x² - 4) = 0

(x - 3)(x² - 2²) = 0

Using the identity (x² - 2²) = (a + b)(a - b),

(x - 3)(x + 2)(x - 2) = 0

x - 3 = 0  or  x + 2 = 0  or  x - 2 = 0

x = 3  or  x = -2  or  x = 2

The given function has three x-intercepts and they are 3, -2 and 2.

Example 5 :

y = e^x - e

Solution :

y = e^x - e

Substitute y = 0 to find the x-intercept.

e^x - e = 0

Add e to both sides.

e^x = e

Take natural logarithm on both sides.

lne^x = lne

Using the power rule of logarithm,

xlne = lne

x(1) = 1

x = 1

The given function has one x-intercept and it is 1.

Example 6 :

y = log₁₀(x + 2)

Solution :

y = log₁₀(x + 2)

Substitute y = 0 to find the x-intercept.

log₁₀(x + 2) = 0

Convert the above equation to exponential.

x + 2 = 10⁰

x + 2 = 1

Subtract 2 from both sides.

x = -1

The given function has one x-intercept and it is -1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.