HOW TO GRAPH CIRCLES

Graph the circles whose equations are given :

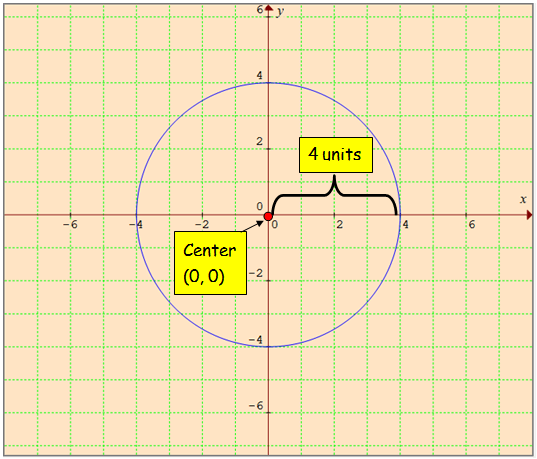
Example 1 :

x² + y² = 16

Solution :

The the given equation is in the form of

x² + y² = r².

Center of the circle is (0, 0). 

r² = 16

r = √16

radius = 4 units

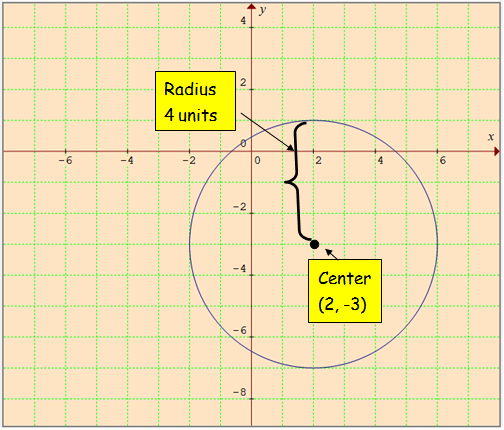
Example 2 :

(x - 2)² + (y + 3)² = 16

Solution :

The the given equation of the circle is in the form of

(x - h)² + (y - k)² = r² ----(1)

Center of the circle is (h, k) and radius is r.

(x - 2)² + (y + 3)² = 16

(x - 2)² + (y - (-3))² = 4² ----(2)

Comparing (1) and (2),

center (h, k) = (2, -3)

r² = 4²

r = 4

radius = 4 units

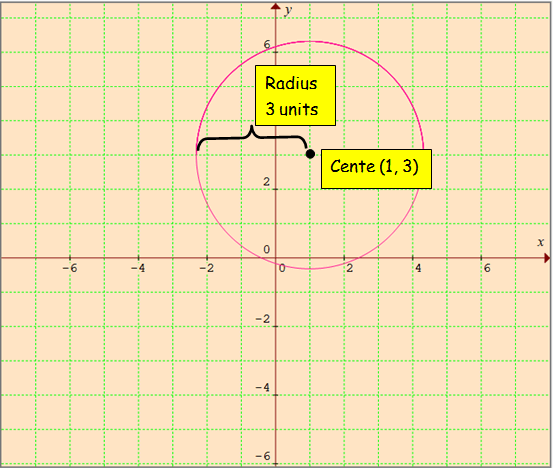
Example 3 :

x² + y² - 2x - 6y + 1 = 0

Solution :

The equation of the  given circle is in general form

x² + y²+ 2gx + 2fy + c = 0 ----(1)

center = (-g, -f)

radius = √(g² + f² - c)

x² + y² - 2x - 6y + 1 = 0 ----(2)

Comparing (1) and (2),

2g = -2 ----> g = -1 ----> -g = 1

2f = -6 ----> f = -3 ----> -f = 3

center (-g, -f) = (1, 3)

radius = √(g² + f² - c)

= √(1² + 3² - 1)

= √(1 + 9 - 1)

= √9

r = 3 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.