HOW TO IDENTIFY IF THE GIVEN MATRIX IS SINGULAR OR NONSINGULAR
A square matrix A is said to be singular if |A| = 0. A square matrix A is said to be non-singular if | A | ≠ 0.
Question 1 :
Identify the singular and non-singular matrices:
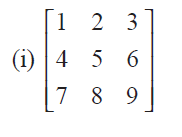
Solution :
In order to check if the given matrix is singular or non singular, we have to find the determinant of the given matrix.
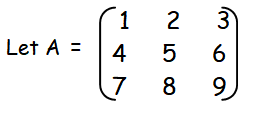
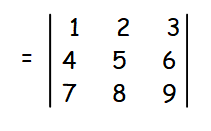 |
= 1[45-48]-2[36-42]+3[32-35] = 1[-3] - 2[-6] + 3[-3] = -3 + 12 - 9 = 0 |
Hence the matrix is singular matrix.
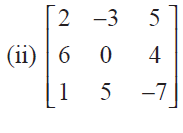
Solution :
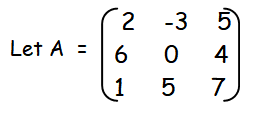
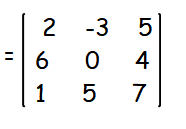 |
= 2[0-20]+3[42-4]+5[30-0] = 2(-20) + 3(38) + 5(30) = -40 + 84 + 150 = 194 |
It is not equal to zero. Hence it is non singular matrix.
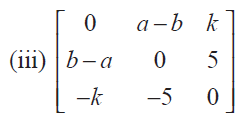
Solution :
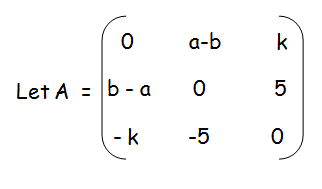
Since the given matrix is skew matrix, |A| = 0.
Hence it is singular matrix.
Question 2 :
Determine the values of a and b so that the following matrices are singular:
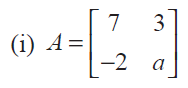
Since it is singular matrix, |A| = 0
|A| = 7a - (-6) = 0
7a + 6 = 0
7a = -6
a = -6/7
Hence the value of a is -6/7.
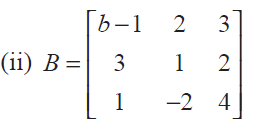
Solution :
Since it is singular matrix, |B| = 0
|B| = (b- 1)[4 + 4] - 2[12 - 2] + 3[-6 - 1]
(b - 1)(8) - 2(10) + 3(-7) = 0
8(b - 1) - 20 - 21 = 0
8(b - 1) - 41 = 0
8(b-1) = 41
b-1 = 41/8
b = (41/8) + 1
= (41 + 8)/8 = 49/8
Hence the value of B is 49/8.
Question 3 :
If cos 2 θ = 0 , determine
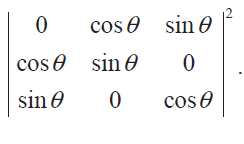
Solution :
cos 2 θ = 0
2θ = cos-1(0 )
2θ = 90 degree
θ = 90/2 = 45 degree
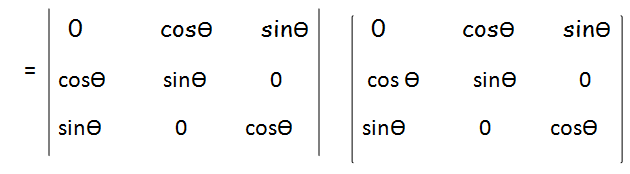
To multiply the above determinants, let us use row by column rule.
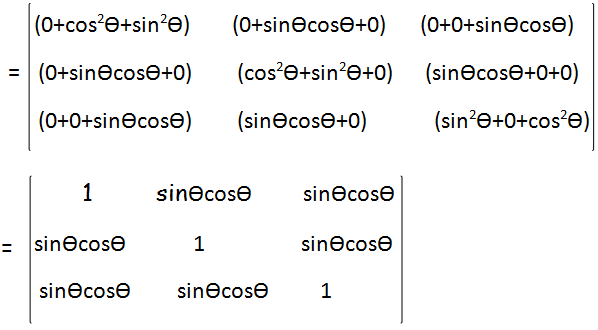
= 1(1 - sin2θcos2θ) - sinθcosθ(sinθcosθ-sin2θcos2θ) + sinθcosθ(sin2θcos2θ-sinθcosθ)
= 1 - sin2θcos2θ - sin2θcos2θ + sin3θcos3θ + sin3θcos3θ - sin2θcos2θ
= 1 - 3sin2θcos2θ + 2sin3θcos3θ
= 1 - 3(sinθcosθ)2 + 2(sinθcosθ)3
By applying 45 degree instead of θ, we get
= 1 - 3(sin 45 cos 45)2 + 2(sin 45 cos 45)3
= 1 - 3((1/√2)(1/√2))2 + 2((1/√2)(1/√2))3
= 1 - 3(1/4) + 2(1/8)
= 1 - (3/4) + (1/4)
= (4 - 3 + 1)/4
= 2/4 = 1/2
Hence the answer is 1/2.
Question 4 :
Find the value of product
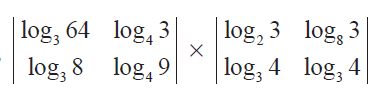
Solution :
In order to find the square of the given determinant, we have to multiply the given determinant by the same.

Here we have followed row by column multiplication.
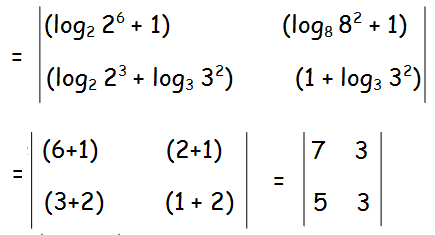
= 21 - 15
= 6
Hence the answer is 6.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

