HOW TO PLOT POLAR COORDINATES

The polar coordinates will be in the form (r, θ). Here r is directed distance.

In other words (r, θ) can be defined where the radius  intersects the angle.

Example :

Plot each point

(a)  (2, π/4)    (b)  (3, 5π/6)

(c)  (-5, π/3)    (d)  (4, π/2)

(e)  (5, 2π)    (f)  (-4, 2π/3)

(g)  (-1, -5π/4)  (h) (2, -4π/3)

Solution :

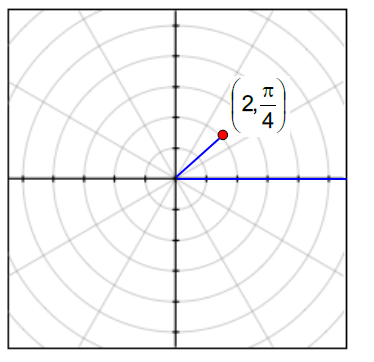
(a)  (2, π/4)

r  =  2 > 0 and θ is positive, so we should move anticlock wise direction.  

(b)  (3, 5π/6)

r  =  3 > 0 and θ is positive, so we should move anticlock wise direction. 

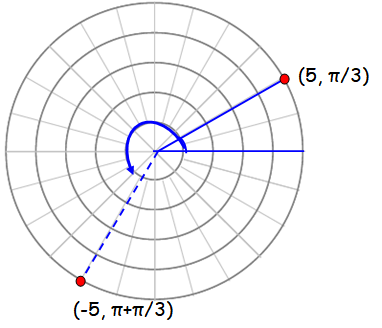
(c)  (-5, π/3) 

r  =  -5 < 0 and θ is positive, so we should move anticlock wise direction. 

To plot a point with a negative radius, find the terminal side of the angle but then measure from the pole in the negative direction of the terminal side.

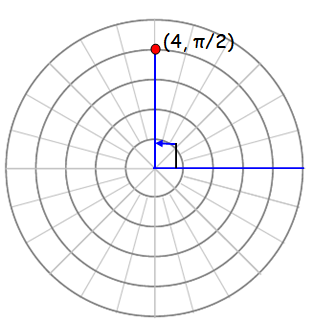
 (d)  (4, π/2)

r  =  4 > 0 and θ is positive, so we should move anticlock wise direction. 

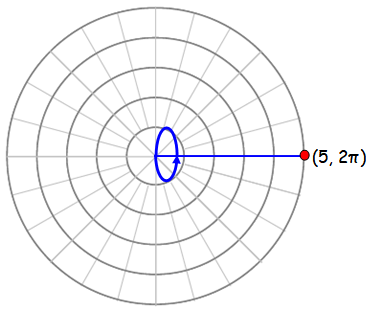
(e)  (5, 2π) 

r  =  5 > 0 and θ is positive, so we should move anticlock wise direction. 

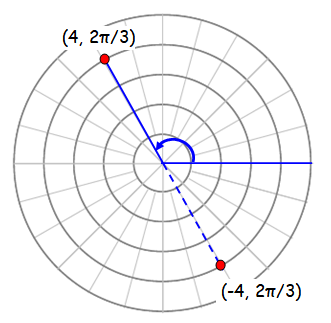
(f)  (-4, 2π/3)

r  =  -4 < 0 and θ is positive, so we should move anticlock wise direction. 

Since it is negative radius, the terminal side is at  (π+2π/3)

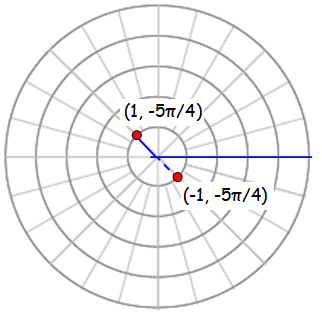
(g)  (-1, -5π/4)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.