HOW TO PROVE THAT THE FUNCTION IS NOT DIFFERENTIABLE

The function is differentiable from the left and right. As in the case of the existence of limits of a function at x₀, it follows that

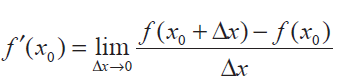
exists if and only if both

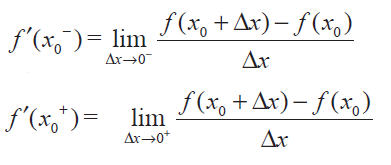
exist and f' (x₀-)  =   f' (x₀+) 

Hence 

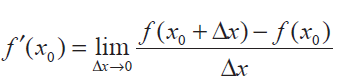
if and only if f' (x₀-)  =   f' (x₀+). If any one of the condition fails then f'(x) is not differentiable at x_0.

From the above statements, we come to know that if f' (x₀-)  ≠  f' (x₀+), then we may decide that the function is not differentiable at x₀.

Question 1 :

Show that the following functions are not differentiable at the indicated value of x.

(i)

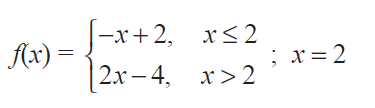
Solution :

f'(2^-)  =  lim _x->2- [(f(x) - f(2)) / (x - 2)]

  =  lim _x->2- [(-x + 2) - (-2 + 2)] / (x - 2)

  =  lim _x->2- -(x - 2) / (x - 2)

  =  lim _x->2- (-1)

  =  -1  -----(1)

f'(2⁺)  =  lim _x->2+ [(f(x) - f(2)) / (x - 2)]

  =  lim _x->2+ [(2x - 4) - (4 - 4)] / (x - 2)

  =  lim _x->2+ 2(x -2) / (x - 2)

  =  2 -----(2)

f'(2^-)  ≠ f'(2⁺) 

Hence the given function is not differentiable at the point x = 2.

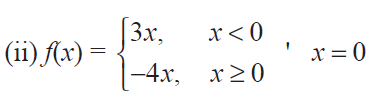
Solution :

f'(0^-)  =  lim _x->0- [(f(x) - f(0)) / (x - 0)]

  =  lim _x->0- [(3x) - 0] / (x - 0)

  =  lim _x->0- (3x/x)

  =  lim _x->0- 3

  =  3  -----(1)

f'(0⁺)  =  lim _x->0+ [(f(x) - f(0)) / (x - 0)]

  =  lim _x->0+ [(-4x) - 0] / (x - 0)

  =  lim _x->0+ (-4x/x)

  =  lim _x->0+ -4

  =  -4 -----(2)

f'(0^-)  ≠ f'(0⁺) 

Hence the given function is not differentiable at the point x = 0.

Question 2 :

The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.

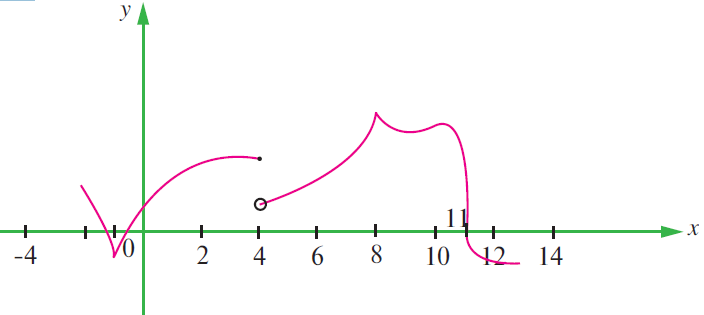
Solution :

If a function is continuous at a point, then it is not necessary that the function is differentiable at that point.

A function f is not differentiable at a point x0 belonging to the domain of f if one of the following situations holds:

(i) f has a vertical tangent at x₀.

(ii) The graph of f comes to a point at x₀ (either a sharp edge ∨ or a sharp peak ∧ )

(iii) f is discontinuous at x₀.

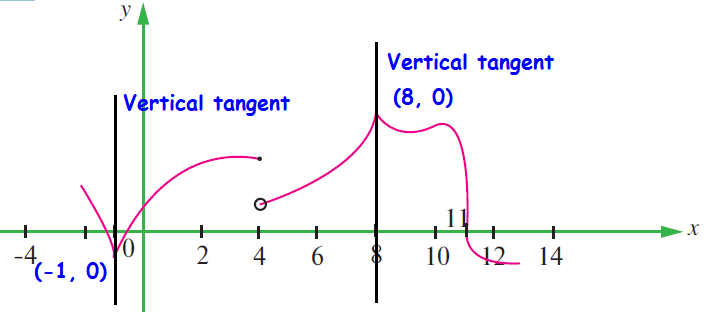
At x = 1 and x = 8, we get vertical tangent (or) sharp edge and sharp peak. So it is not differentiable at x = 1 and 8.

At x = 4,  we hjave a hole. Hence it is not continuous at x = 4.

At x = 11, we have perpendicular tangent. So it is not differentiable at x =  11.

Question 3 :

If f(x) = |x + 100| + x², test whether f'(-100) exists.

Solution :

f'(-100^-)  =  lim _x->-100- [(f(x) - f(-100)) / (x - (-100))]

  =  lim _x->-100- [(-(x + 100)) + x²) - 100²] / (x + 100)

  =  lim _x->-100- [(-(x + 100)) + (x² - 100²)] / (x + 100)

  =  lim _x->-100- [(-(x + 100)) + (x + 100) (x -100)] / (x + 100)

  =  lim _x->-100- (x + 100)) [-1 + (x -100)] / (x + 100)

  = [-1 + (-100 -100)] 

=  -201   --------(1)

f'(-100⁺)  =  lim _x->-100+ [(f(x) - f(-100)) / (x - (-100))]

  =  lim _x->-100- [(x + 100)) + x²) - 100²] / (x + 100)

  =  lim _x->-100- [(x + 100)) + (x² - 100²)] / (x + 100)

  =  lim _x->-100- [(x + 100)) + (x + 100) (x -100)] / (x + 100)

  =  lim _x->-100- (x + 100)) [1 + (x -100)] / (x + 100)

  =  lim _x->-100- (x - 99) 

=  -199   --------(2)

Hence f'(-100) does not exists.

Question 4 :

Examine the differentiability of functions in R by drawing the diagrams.

(i) | sin x | 

Solution :

Graph of y = sin x

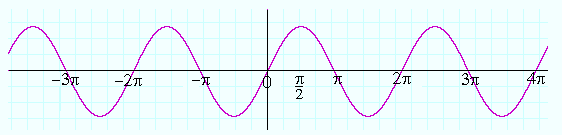
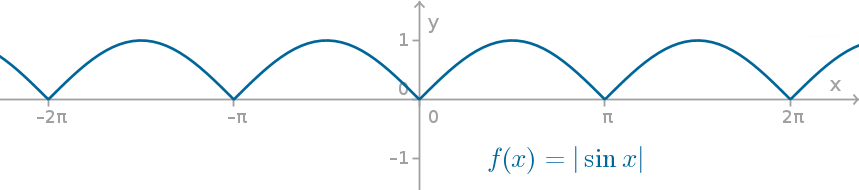
There is vertical tangent for nπ. Hence it is not differentiable at x = nπ, n ∈ z

(ii) | cos x|

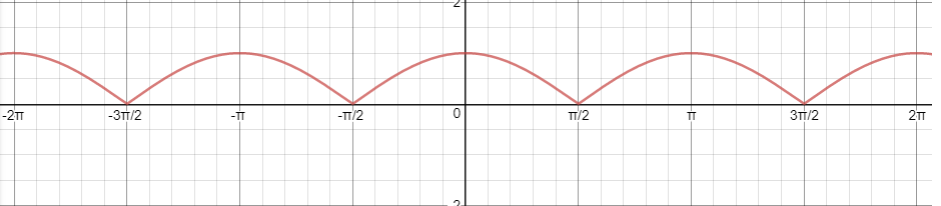
Solution :

There is vertical tangent for (2n + 1)(π/2). Hence it is not differentiable at x = (2n + 1)(π/2), n ∈ z

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.