HOW TO PROVE THE GIVEN 4 VECTORS ARE COPLANAR

To prove the given 4 vectors are coplanar, we have to form three vectors using those vectors. Then we have to check whether there is any linear relationship.

Let us look into a example problem to understand the concept much better.

How to Prove the Given 4 Vectors are Coplanar - Practice Question

Question 1 :

Show that the points whose position vectors 4i + 5j + k, − j − k, 3i + 9j + 4k and −4i + 4j + 4k are coplanar.

Solution :

Let OA vector  =  4i + 5j + k

OB vector  =  − j − k

OC vector  =  3i + 9j + 4k

OD vector  =  −4i + 4j + 4k

AB vector  =  OB vector - OA vector

  =  (-j-k) - (4i + 5j + k)

  =  -4i -j - 5j - k - k

  =  -4i -6j - 2k

AC vector  =  OC vector - OA vector

  =   (3i + 9j + 4k) - (4i + 5j + k)

  =  3i - 4i + 9j - 5j + 4k - k

  =  -i + 4j + 3k

AD vector  =  OD vector - OA vector

  =   (−4i + 4j + 4k) - (4i + 5j + k)

  =  -4i - 4i + 4j - 5j + 4k - k

  =  -8i - j + 3k

 -4i -6j - 2k  =  s(-i + 4j + 3k) + t(-8i - j + 3k)

-4  =  -s - 8t  -------(1)

-6  =  4s - t  -------(2)

-2  =  3s + 3t -------(3)

Multiply the (1) by 4 and add (1) + (2)

-4s - 32t + 4s - t  =  -16 - 6

-33t  =  -22

t  =  2/3

Applying the value of t in (1)

-s - 8(2/3)  =  -4

-s - (16/3)  =  -4

-s  =  -4 + (16/3)

-s  =  (-12 + 16)/3

-s  =  4/3

s  =  -4/3

By applying the value of s and t, we get

-2  =  3(-4/3) + 3(2/3) 

-2  =  -4 + 2

-2  =  -2

Hence given vectors are coplanar.

By taking determinants, easily we may check whether they are coplanar or not.

If |AB  AC  AD|  =  0, then A, B, C and D are coplanar.

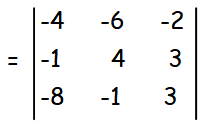
  =  -4[12+3] + 6[-3+24] - 2[1+32]

  =  -4[15] + 6[21] - 2[33]

  =  -60 + 126 - 66

  =  -126 + 126

  =  0

Hence the given points are coplanar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.