HOW TO PROVE TWO RIGHT TRIANGLES ARE CONGRUENT

Two triangles are congruent if they have the same three sides and exactly the same three angles. Two right triangles can be considered to be congruent, if they satisfy one of the following theorems.

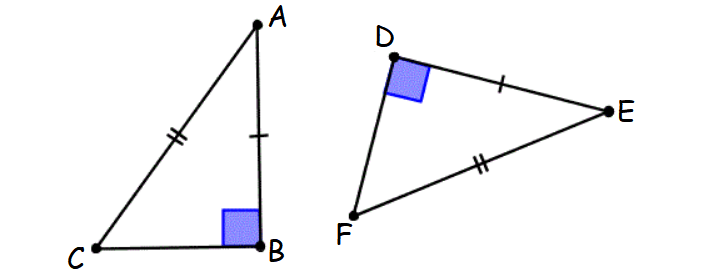
Theorem 1 : Hypotenuse-Leg (HL) Theorem :

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

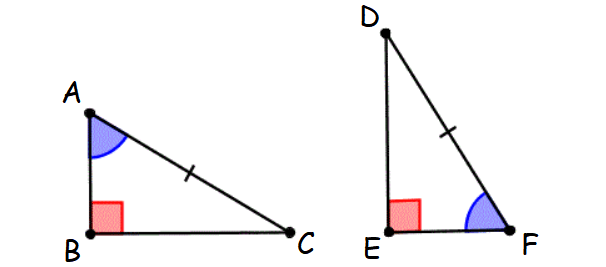
Theorem 2 : Leg-Acute (LA) Angle Theorem :

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

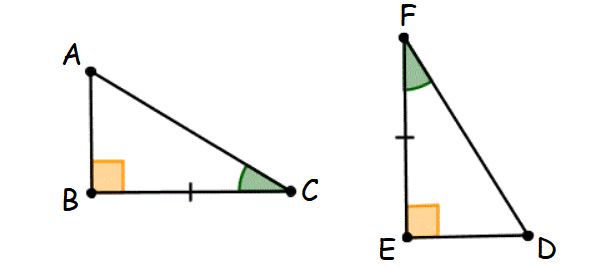
Theorem 3 : Hypotenuse-Acute (HA) Angle Theorem :

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

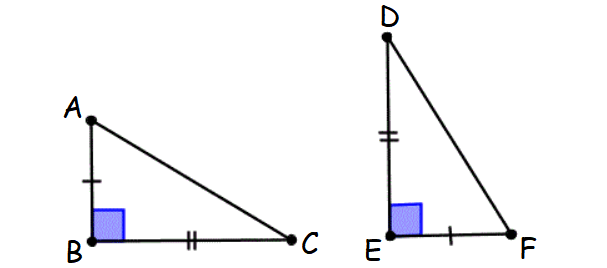
Theorem 4 : Leg-Leg (LL) Theorem :

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

Solved Examples

Example 1 :

Check whether two triangles ABC and CDE are congruent.

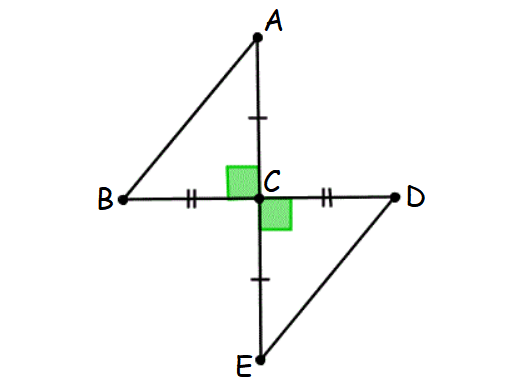
Solution :

(i) Triangle ABC and triangle CDE are right triangles. Because they both have a right angle. 

(i) AC  =  CE (Leg)

(ii) BC  =  CD (Leg)

Hence, the two triangles ABC and CDE are congruent by Leg-Leg theorem. 

Example 2 :

Check whether two triangles PQR and RST are congruent.

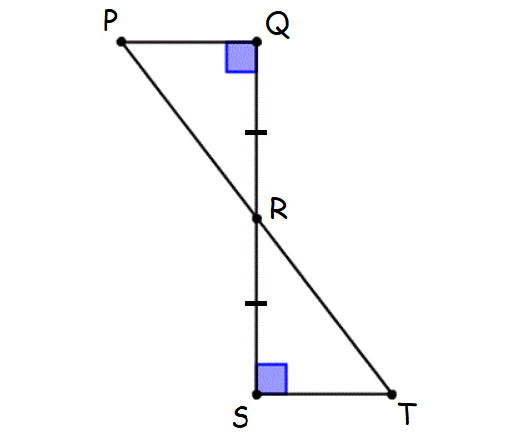
Solution :

(i) Triangle PQR and triangle RST are right triangles. Because they both have a right angle. 

(ii) QR  =  RS (Given)

(iii) ∠PRQ  =  ∠SRT (Vertical Angles)

Hence, the two triangles PQR and RST are congruent by Leg-Acute (LA) Angle theorem. 

Example 3 :

Check whether two triangles ABD and ACD are congruent.

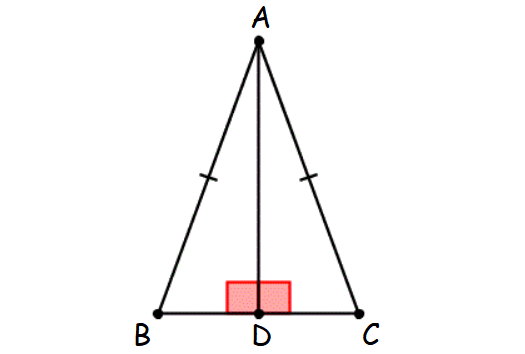
Solution :

(i) Triangle ABD and triangle ACD are right triangles. Because they both have a right angle. 

(i) AB  =  AC (Hypotenuse)

(ii) AD  =  AD (Common side, Leg)

Hence, the two triangles ABD and ACD are congruent by Hypotenuse-Leg (HL) theorem. 

Example 4 :

Check whether two triangles OPQ and IJK are congruent.

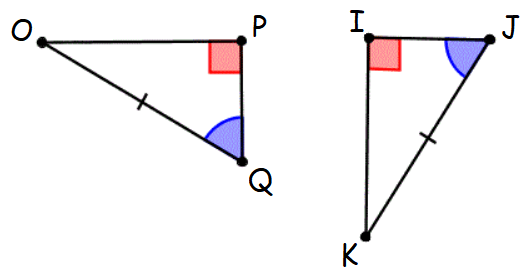
Solution :

(i) Triangle OPQ and triangle IJK are right triangles. Because they both have a right angle. 

(ii) OQ  =  JK (Hypotenuse)

(iii) ∠Q  =  ∠J (Given)

Hence, the two triangles OPQ and IJK are congruent by Hypotenuse-Acute (HA) Angle theorem. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.