HOW TO SIMPLIFY COMPLEX RATIONAL EXPRESSIONS

Definition of complex rational expressions :

Complex rational expressions, also called complex fractions, have numerators or denominators containing one or more fractions.

Method 1 : (Using division method)

If the given complex fractions have a single fraction in both numerator and denominator, then multiply the fraction in the numerator by the reciprocal of the denominator.

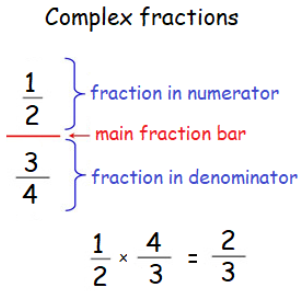
Method 2 : (Using LCM method)

Step 1 :

If the given complex fractions have a two or more fractions they are added or subtracted in both numerator and denominator with like denominators, write the denominator once and add the numerators.

Step 2 :

If the given complex fractions have two or more fractions and they are added or subtracted in both numerator and denominator with unlike denominators, then we have to use least common multiple and combine them.

Step 3 :

Simplify the numerator and denominator.

Step 4 :

To get the result, Multiply the fraction in the numerator by the reciprocal of the denominator

Method 3 : (Using cross multiplication method)

Step 1 :

If the given complex fractions have a one fractions and one integer, then we have to apply the cross multiplication method.

Step 2 :

Simplify the numerator and denominator.

Step 3 :

To get the result, multiply the fraction in the numerator by the reciprocal of the denominator

Simplify :

Problem 1 :

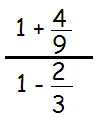
Solution :

By using cross multiplication, we get

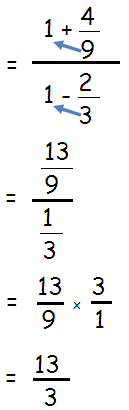
Problem 2 :

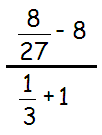
Solution :

By using cross multiplication, we get

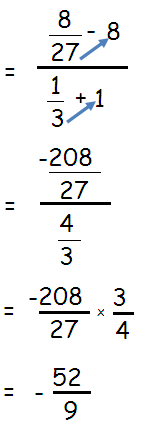
Problem 3 :

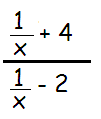
Solution :

By using cross multiplication, we get

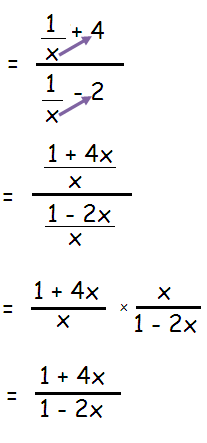
Problem 4 :

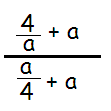
Solution :

By cross multiplication, we get

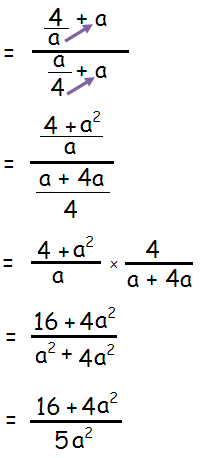
Problem 5 :

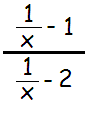
Solution :

By cross multiplication, we get

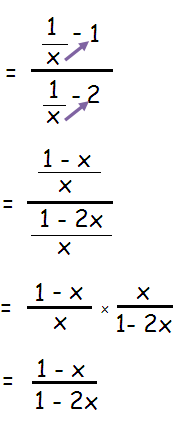
Problem 6 :

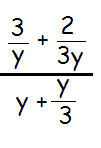
Solution :

Problem 7 :

$simplifying-complex-fracq1$

Solution :

Simplifying ((u + 2) / 4) - (2/3) :

= [3(u + 2) - 2(4)]/12

= (3u + 6 - 8)/12

= (3u - 2) / 12

Applying this simplification in the question, we get
= (3u - 2) / 12 / (u - 2)

= (3u - 2) / 12(u - 2)

Problem 8 :

$simplifying-complex-fracq2.png$

Solution :

4/x is already in simplified form.

Denominator :

= 1/2 - x²/2

= (1 - x²)/2

= (1 + x)(1 - x)/2

Applying in the question, we get

= (4/x) / (1 + x)(1 - x)/2

= 4/x ⋅ 2/(1 + x)(1 - x)

= 8/x(1 + x)(1 - x)

Problem 9 :

$simplifying-complex-fracq3$

Solution :

Simplifying the numerator :

2/(x + 5) + 4/(x + 3)

= 2(x + 3) + 4(x + 5) / (x + 5)(x + 3)

= (2x + 6 + 4x + 20) / (x + 5)(x + 3)

= (6x + 26) / (x + 5)(x + 3) ------(1)

Simplifying the denominator :

(3x + 13) / (x² + 8x + 15)

= (3x + 13) / (x + 3)(x + 5)------(2)

(1) / (2)

= (6x + 26) / (x + 5)(x + 3) / (3x + 13) / (x + 3)(x + 5)

= 2(3x + 13)/ (x + 5)(x + 3) ⋅ (x + 3)(x + 5)/ (3x + 13)

= 2

Problem 10 :

$simplifying-complex-fracq4.png$

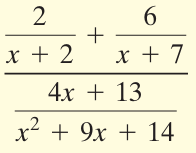
Solution :

Simplifying the numerator :

2/(x + 2) + 6/(x + 7)

= [2(x + 7) + 6(x + 2)]/(x + 2)(x + 7)

= (2x + 14 + 6x + 12)/(x + 2)(x + 7)

= (8x + 26) / (x + 2)(x + 7) -----(1)

Simplifying the denominator :

= (4x + 13) / (x² + 9x + 14)

= (4x + 13) / (x + 2)(x + 7) -----(2)

(1) / (2)

= (8x + 26) / (x + 2)(x + 7) / (4x + 13) / (x + 2)(x + 7)

= [2(4x + 13) / (x + 2)(x + 7)] ⋅ [(x + 2)(x + 7) / (4x + 13)]

= 2

Problem 11 :

$simplifying-complex-fracq5.png$

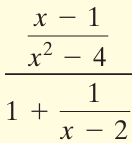
Solution :

Simplifying the numerator :

= (x - 1) / (x² - 2²)

= (x - 1) / (x + 2)(x - 2) --------(1)

Simplifying the denominator :

= 1 + (1/(x - 2))

= (x - 2 + 1) / (x - 2)

= (x - 1) / (x - 2) --------(2)

(1) / (2)

= (x - 1) / (x + 2)(x - 2) / (x - 1) / (x - 2)

= [(x - 1) / (x + 2)(x - 2)] ⋅ [(x - 2) / (x - 1)]

= 1/(x + 2)

Problem 12 :

[x / (3x - 2)] ÷ [x / (9x² - 4)]

Solution :

= [x / (3x - 2)] ÷ [x / ((3x)² - 2²)]

= [x / (3x - 2)] ÷ [x / (3x + 2) (3x - 2)]

= [x / (3x - 2)] ⋅ [(3x + 2) (3x - 2) / x]

= 3x + 2

Problem 13 :

[(x - 5) - (18/(x + 2))] ÷ [(x + 7) + (6/(x + 2))]

Solution :

= [(x - 5) - (18/(x + 2))] ÷ [(x + 7) + (6/(x + 2))]

= [(x - 5)(x + 2) - 18]/(x + 2) ÷ [(x + 7)(x + 2) + 6]/(x + 2)

= [(x - 5)(x + 2) - 18/(x + 2)] ⋅ [(x + 2)/(x + 7)(x + 2) + 6]

= (x² - 3x - 10 - 18)/(x² + 9x + 14 + 6)

= (x² - 3x - 28)/(x² + 9x + 20)

= (x - 7)(x + 4) / (x + 5)(x + 4)

= (x - 7) / (x + 5)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

HOW TO SIMPLIFY COMPLEX RATIONAL EXPRESSIONS

Recent Articles

Digital SAT Math Problems and Solutions (Part - 151)

AP Calculus BC Problems with Solutions

Digital SAT Math Problems and Solutions (Part - 150)